
平面図形の面積の求め方の公式
■多角形の面積の求め方
長方形=縦×横
正方形=1辺×1辺=対角線×対角線÷2
平行四辺形=底辺×高さ
台形=(上底+下底)×高さ÷2
ひし形(対角線直交四角形)の面積=対角線×対角線÷2
三角形=底辺×高さ÷2
●円の面積の求め方
円周=直径×円周率(3.14)=半径×2×円周率(3.14)
円の面積=半径×半径×円周率(3.14)
■おうぎ形の面積の求め方
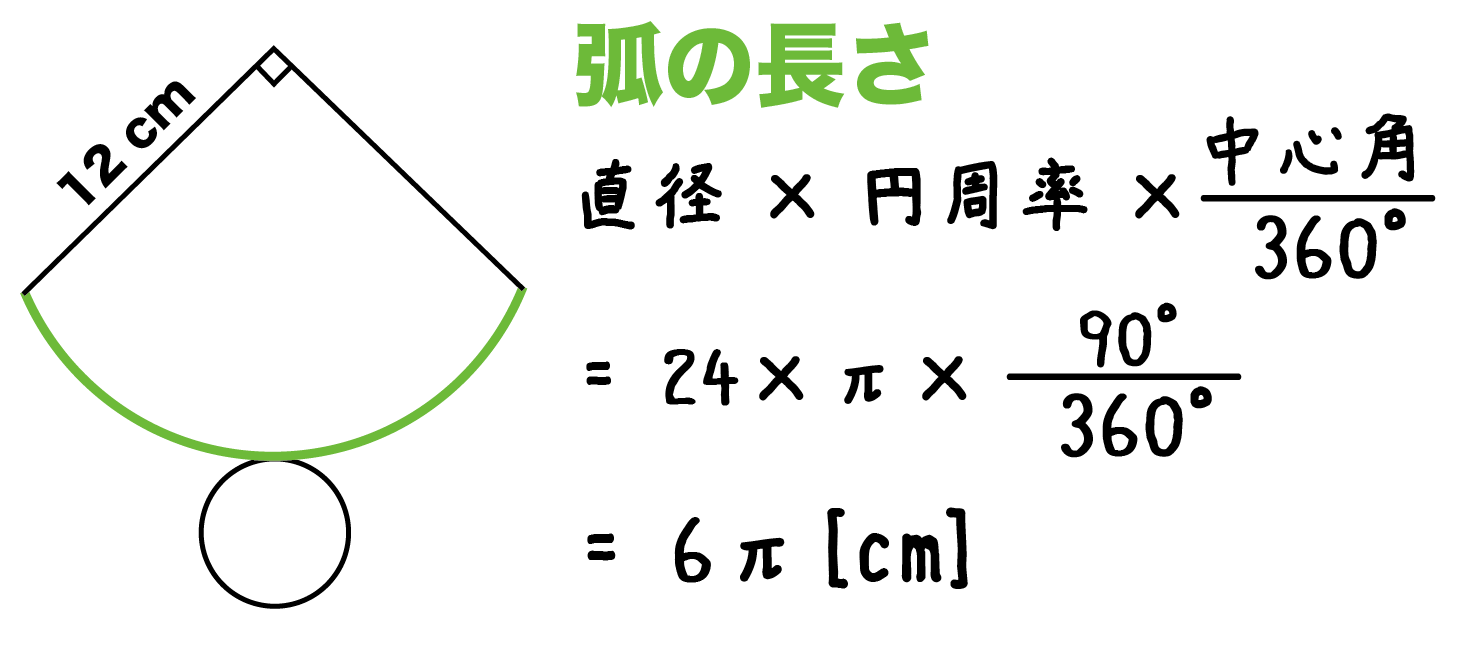
おうぎ形の弧の長さ=円周×中心角/360=直径×3.14×中心角/360
おうぎ形の面積=円の面積×中心角/360=半径×半径×円周率×中心角/360
レンズ形の面積=

(画像出典:「中学受験 算数の基本問題」)
上記が「図形」の面積等を求める「基本公式」になります。
基本だけの問題というのはあまり出ませんが、基本ができて
いないと応用はできませんので、確実にきちんと覚えておき
ましょう。
台形=(上底+下底)×高さ÷2

上記の台形の面積は
台形=(上底+下底)×高さ÷2
=(3+7)×5÷2
=25cm2
ひし形(対角線直交四角形)の面積=対角線×対角線÷2

ひし形(対角線直交四角形)の面積=対角線×対角線÷2
ですから、
6×4÷2=12cm2
円周=直径×円周率(3.14)=半径×2×円周率(3.14)

円周=直径×円周率(3.14)=半径×2×円周率(3.14)
円の面積=半径×半径×円周率(3.14)

円の面積=半径×半径×円周率(3.14)
おうぎ形の弧の長さ=円周×中心角/360=直径×3.14×中心角/360

おうぎ形の弧の長さ=円周×中心角/360=直径×3.14×中心角/360
(3+3)×3.14×120/360
=18.84×1/3
=18.84/3
=6.28
答え)6.28
おうぎ形の面積=円の面積×中心角/360=半径×半径×円周率×中心角/360


おうぎ形の面積=円の面積×中心角/360=半径×半径×円周率×中心角/360
6×6×3.14×60/360
=36×3.14×1/6
=113.04×1/6
=18.84
答え)18.84cm2
レンズ形の面積は三角形とおうぎ形の組み合わせ

(画像出典:「中学受験 算数の基本問題」)
まとめ
以上、
平面図形の面積の求め方(基本編)―「中学受験+塾なし」の勉強法・教え方
でした。
中学受験では「基本」は”できて当然”というのが基本となって
いるのが現実です・・・。ですので、確実にできるようにして
おきましょう。