「水量の変化とグラフ」は水そうに水を入れていく際に
「図」と「グラフ」があって、それらを読み解く必要があります。
要素として、「図形」「割合と比」「速さ」「つるかめ算」等々の
力が必要になる総合的な問題と言えます。
何度も読んで、問題を解きマスターしていってください。
「水量の変化とグラフ」は水そうに水を入れていく系問題でまずやること
★図とグラフから分かる事を「平面図」にしていく★
図の出典:『塾技100』p132
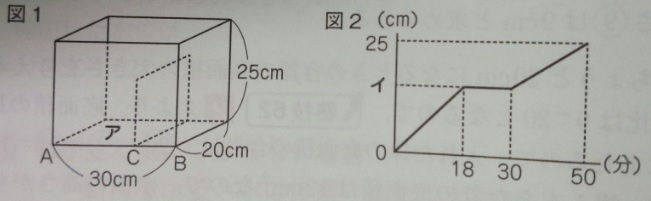
こんな感じの図とグラフが出ます。
★「水量の変化とグラフ」は水そうに水を入れていく系問題でやること★
1 水そうを正面から見た平面図を書く
2 グラフから分かる水面の高さをすべて書く
3 それぞれの部分について分かる(かかる)時間を書く
*これを正確にできるようになるとこの種の問題の多くは解けます
★図とグラフから分かる事を「平面図」にしていく★
この図とグラフでさっそく練習してみてください。
問題)図1の容器のアの部分に毎分一定の割合で水を入れたとき、水を入れた
時間とアの部分の水面の高さが図2のようになりました。この時、容器のACと
BCの長さの比、および(仕切りの高さ)イを求めなさい。

図の出典:『塾技100』p132
1 水そうを正面から見た平面図を書く
2 グラフから分かる水面の高さをすべて書く
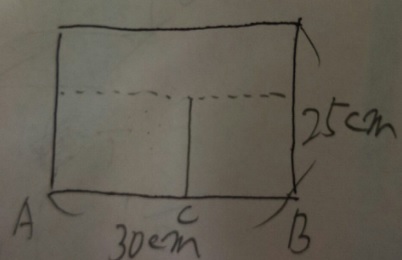
「平面図」である事が大事です。また上記の図にはありませんが、
「水が入ってくる所」(AとCの間の上部)を書いておいても良いです。
「水面の高さ」は点線部分と一番上の線です。
しきいがふたつあるような水そうの場合は線がさらに増えます。
いずれにせよ「グラフから分かる水面の高さをすべて書く」事が大事です。
3 それぞれの部分について分かる(かかる)時間を書く
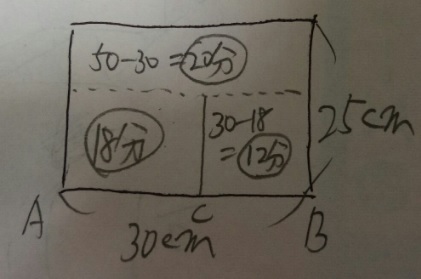
まずはここまでできるようになる事が大事です。
★「水量の変化とグラフ」は水そうに水を入れていく系問題でやること★
1 水そうを正面から見た平面図を書く
2 グラフから分かる水面の高さをすべて書く
3 それぞれの部分について分かる(かかる)時間を書く
*これを正確にできるようになるとこの種の問題の多くは解けます
★図とグラフから分かる事を「平面図」にしていく★

水量の変化とグラフ(水そうに水をいれいく系の問題)のテクニック・解き方

図の出典:『塾技100』p132
(同じ高さまで水を入れるとき)
★かかる時間の比は底面積の比と同じ★
★(かかる時間の比は)奥行き一定(の直方体の容器)なら横の長さの比と同じ★
*これは想像・イメージすると分かるのでは?
★底面積が一定なら水を入れる時間の比と水位の比は同じ★
*これもイメージすると分かるのでは?
やってみましょう。
問題)図1の容器のアの部分に毎分一定の割合で水を入れたとき、水を入れた
時間とアの部分の水面の高さが図2のようになりました。この時、容器のACと
BCの長さの比、および(仕切りの高さ)イを求めなさい。

図の出典:『塾技100』p132

★(かかる時間の比は)奥行き一定(の直方体の容器)なら横の長さの比と同じ★
なので、AC:CB=18:12=3:2
★底面積が一定なら水を入れる時間の比と水位の比は同じ★
なので、イまでの高さにかかる時間12+18=30分とイから25cmまでにかかる時間
20分の比率が水位(高さ)の比率と同じになる。
30:20→3:2 割合5=25cm、割合1=5cm、割合3=15cm イの高さは15cm
答え)ACとBCの長さの比は3:2、イの高さは15cm
水量の変化とグラフ(水そうに水をいれいく系の問題)の中学入試問題等
問題)図のように、たて30㎝、横60㎝、高さ40㎝の水そうが、
底面に垂直な2枚の板(板1、板2)で仕切られています。
この水そうに毎秒240㎤の割合で右側から水を注ぎ、辺ABで
水の深さを測ったところ、時間と水の深さの関係はグラフのよう
になりました。これについて、次の問いに答えなさい。
(1) BC、CDの長さを求めなさい。
(2) 板1、板2の高さを求めなさい。
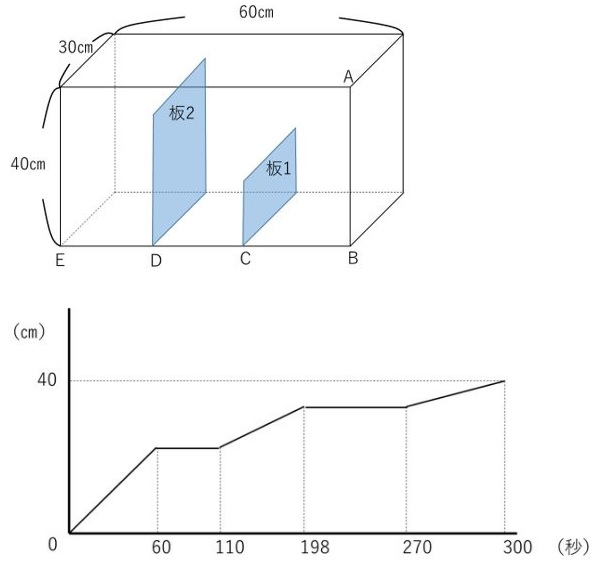
出典:https://www.chugakujuken.com/koushi_blog/kamei/20190625.html
★「水量の変化とグラフ」は水そうに水を入れていく系問題でやること★
1 水そうを正面から見た平面図を書く
2 グラフから分かる水面の高さをすべて書く
3 それぞれの部分について分かる(かかる)時間を書く
*これを正確にできるようになるとこの種の問題の多くは解けます
★図とグラフから分かる事を「平面図」にしていく★
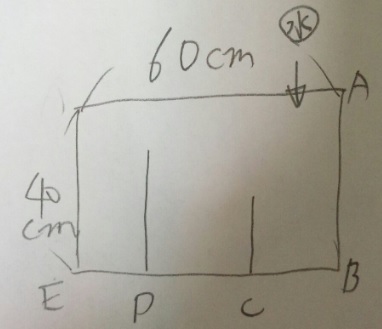

これが書ければ、後は単純な計算です。問題)図のように、たて30㎝、横60㎝、高さ40㎝の水そうが、
底面に垂直な2枚の板(板1、板2)で仕切られています。
この水そうに毎秒240㎤の割合で右側から水を注ぎ、辺ABで
水の深さを測ったところ、時間と水の深さの関係はグラフのよう
になりました。これについて、次の問いに答えなさい。
(1) BC、CDの長さを求めなさい。
(2) 板1、板2の高さを求めなさい。

出典:https://www.chugakujuken.com/koushi_blog/kamei/20190625.html
(同じ高さまで水を入れるとき)
★かかる時間の比は底面積の比と同じ★
★(かかる時間の比は)奥行き一定(の直方体の容器)なら横の長さの比と同じ★
*これは想像・イメージすると分かるのでは?
★底面積が一定なら水を入れる時間の比と水位の比は同じ★
*これもイメージすると分かるのでは?
(1) BC、CDの長さを求めなさい。
★(かかる時間の比は)奥行き一定(の直方体の容器)なら横の長さの比と同じ★
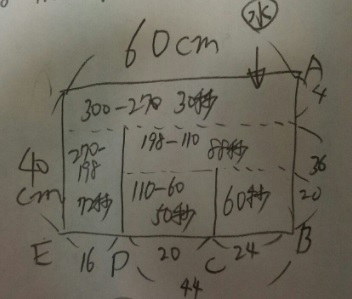
1)ED72秒:BD198秒→割合4:割合11 割合15=60cm、割合1=4cm、ED=16cm、BD=44cm
2)DC50秒:BC60秒→5:6、BD=44cmなので割合①=4cm、CD=20cm、BC=24cm
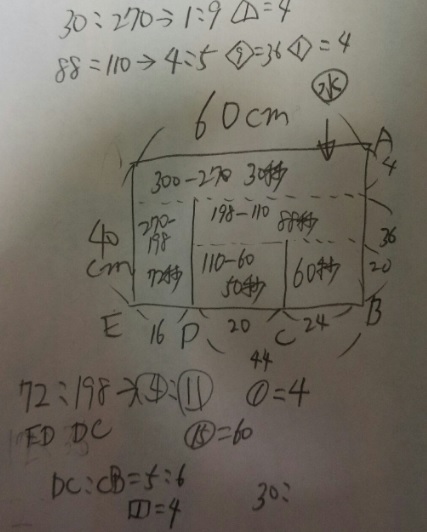

(2) 板1、板2の高さを求めなさい。
★底面積が一定なら水を入れる時間の比と水位の比は同じ★
1)底面積が同じ→横の長さが同じでなければなりません
板2まで埋まるのが270秒、そこからAまでが30秒→9:1 高さ40cmなので割合1=4cm
板2まで36cm、そこからAまで4cm
(横の長さは60cmなので同じです)
2)板1が埋まるまで110秒、そこから板2の高さまで88秒→5:4
板2まで36cmなので、割合1=4cm、板1まで20cm、板1から板2まで16cm

答え)BC=24cm、CD=20cm 板1:20cm、板2:36cm
問題)海城中学(問題文はワイが変えてます)
毎秒8立方cmで水をウから注ぎます。グラフは入れ始めてからの時間と
イの部分の水面の高さの関係です。
アとイとウの底面積の比をもっとも簡単な整数の比で求めてください。
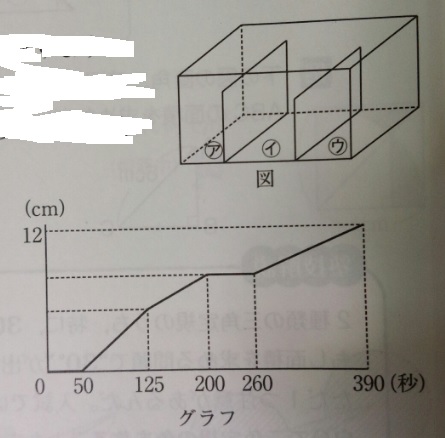
★「水量の変化とグラフ」は水そうに水を入れていく系問題でやること★
1 水そうを正面から見た平面図を書く
2 グラフから分かる水面の高さをすべて書く
3 それぞれの部分について分かる(かかる)時間を書く
*これを正確にできるようになるとこの種の問題の多くは解けます
★図とグラフから分かる事を「平面図」にしていく★
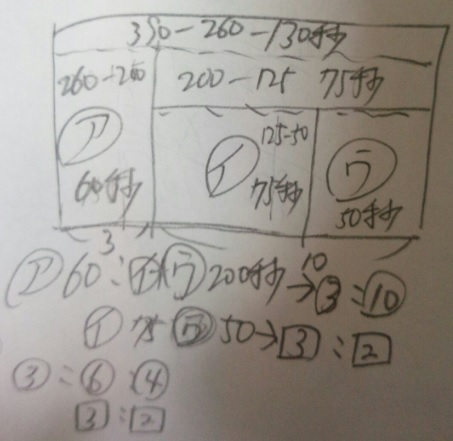
これが書ければ解けます。
★かかる時間の比は底面積の比と同じ★なので「底面積」が同じ部分の時間の比を出す。
1)「ウ」から水を入れてることと、グラフが「イ」の部分の高さであるひっかけに気をつけて
2)「ア」60秒:「イ+ウ」200秒→③:⑩
3)「イ」75秒:「ウ」50秒→「3」:「2」
4)連比?と思いましたが、⑩が「3」+「2」なので簡単ですね?
⑩が「6」「4」と言えます。3:6:4
答え)3:6:4

まとめ


★「水量の変化とグラフ」は水そうに水を入れていく系問題でやること★
1 水そうを正面から見た平面図を書く
2 グラフから分かる水面の高さをすべて書く
3 それぞれの部分について分かる(かかる)時間を書く
*これを正確にできるようになるとこの種の問題の多くは解けます
★図とグラフから分かる事を「平面図」にしていく★
(同じ高さまで水を入れるとき)
★かかる時間の比は底面積の比と同じ★
★(かかる時間の比は)奥行き一定(の直方体の容器)なら横の長さの比と同じ★
*これは想像・イメージすると分かるのでは?
★底面積が一定なら水を入れる時間の比と水位の比は同じ★
*これもイメージすると分かるのでは?
問題をたくさん解いて慣れていきましょう。