線分図―図を書くと分かる
「算数」の重要なテクニックとして、
・図(線分図)を書くと分かる・
というものがあります。線分図=線で分けた図、です。
線分図を書くテクニック
1 頭を揃えて書く
2 分かっている数字を正確に書く
3 「差」が分かるようにする:補助線を引く
4 全体の割合・比率・倍率を書き込む
5 「差」が全体の中でどれくらいの割合・比率・倍率なのか見抜く
6 あとは、「足し算」「引き算」「掛け算」「割り算」で答えを出す
7 「何年後」の場合は〔そろえた頭の)左に伸ばす
8 「何年前」の場合は〔そろえた頭を)縮める

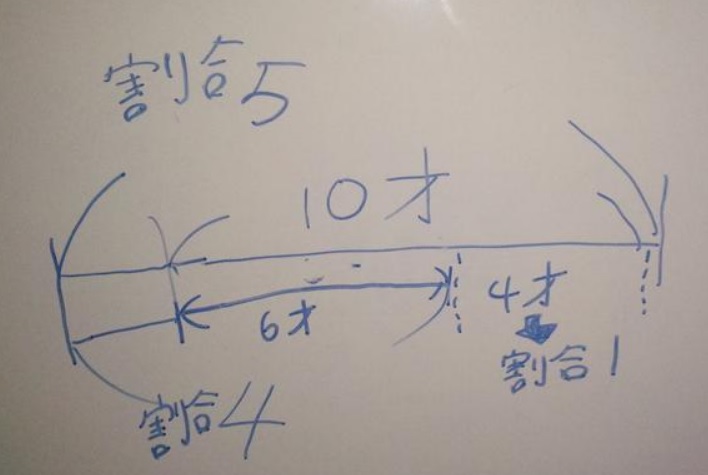
こういうものです(筆者撮影・小学校4年生の子供が書いたもの)
実際に自分で線分図を書いて解いてみましょう。
問題)
10歳と6歳の姉妹がいます、この姉妹の年齢差が5対4
になるのは何年後ですか?
いわゆる「年齢算」というものですね。
線分図を書くと良く分かります。
線分図を書いて解くためのテクニック
線分図を書くテクニック
1 頭を揃えて書く
2 分かっている数字を正確に書く
3 「差」が分かるようにする:補助線を引く
4 全体の割合・比率・倍率を書き込む
5 「差」が全体の中でどれくらいの割合・比率・倍率なのか見抜く
6 あとは、「足し算」「引き算」「掛け算」「割り算」で答えを出す
7 「何年後」の場合は〔そろえた頭の)左に伸ばす
8 「何年前」の場合は〔そろえた頭を)縮める
問題)
10歳と6歳の姉妹がいます、この姉妹の年齢差が5対4
になるのは何年後ですか?
であれば、

まずは、
「1頭をそろえて→2分かっている数字」を書きます。
姉が10歳、妹が6歳ですね。6歳は10歳の半分よりも1大きいので、
できたら、それくらいの位置まで線を引いた方が混乱しません。
次に「3 「差」が分かるにようにする:補助線を引く」です。

妹の6歳の右側は、10歳-6歳=4歳ですので、「4歳」と書いておきます。
このように「差」を出すというのは線分図の最初のポイントです。
次も線分図・年齢算のポイントの一つですが、
「4 全体の割合・比率・倍率を書き込む」
です。
この部分でつまずく小学校4年生などがいるかと思いますので、
その場合、簡単な問題を多数解くことをオススメします。

この問題の場合、「何年後」という問いなので、線分図を伸ばします。
その時のテクニックとして、
7「何年後」の場合は〔そろえた頭の)左に伸ばす
事が大事です。見やすいからです。
(「何年前」の場合は(頭を)縮める)
揃っていない右側を伸ばすと混乱します。
問題)
10歳と6歳の姉妹がいます、この姉妹の年齢差が5対4
になるのは何年後ですか?
ですから、姉の「当初の10歳+何年後」までの年齢が「割合5」
になります。そして、妹の「当初の6歳+何年後」までの年齢は、
「割合4」になります。

すると二人の現在の年齢差である、10-6=4歳は割合1である事
が線分図を書くと読み取れます(ここを「読み取る」訓練が線分図・
年齢算では一番大事です)。
この問題では割合1=4歳です。
与えられた数字を図〔線分図〕にする事で、新たな何が分かるかと
言う視点が算数のセンスであり、テクニックと言えます。
ここでは、「割合1=4歳」という事です。

すると、下記の様に、求めるべき数字〔何年後)の「A」は、
上段の線分図から式1)であることが、下段の線分図から式2)であることが分かります。
式1)割合5-10=A
式2)割合4-6=A
そして、割合1=4歳(4)です。

割合5は割合1の5倍(割合5=割合1×5)ですし、割合4は割合1の4倍です。
それぞれの式に、割合1の数値4を入れます。
1)4×5-10=A→20-10=A
2)4×4-6=A→16-6=A
A=10
です。答え10年後。
合っているのか検算しましょう。
10歳+10年後=20歳
6歳+10年後=16歳
20/16→5/4
5対4の年齢差になっていますね。
このように年齢算・線分図は、基本的な問題はある程度
パターン化して解く事ができますので、まずは、基本的な問題を
多数解いて、「線分図・年齢算」に慣れる事が大事です。
慣れてきたら、応用問題を解いていきましょう。
線分図・年齢算の問題
線分図を書くテクニック
1 頭を揃えて書く
2 分かっている数字を正確に書く
3 「差」が分かるようにする:補助線を引く
4 全体の割合・比率・倍率を書き込む
5 「差」が全体の中でどれくらいの割合・比率・倍率なのか見抜く
6 あとは、「足し算」「引き算」「掛け算」「割り算」で答えを出す
7 「何年後」の場合は〔そろえた頭の)左に伸ばす
8 「何年前」の場合は〔そろえた頭を)縮める
問題)49歳と9歳の親子の年齢差が3倍になるのは何年後ですか?
線分図を書きます。

線分図を書きます(小学校4年生が書いたもの)
1 頭を揃えて書く
2 分かっている数字を正確に書く
3 「差」が分かるようにする:補助線を引く
4 全体の割合・比率・倍率を書き込む
ここまでができるようになるためには、まずは上記のような基本
問題を練習しましょう。
5 「差」が全体の中でどれくらいの割合・比率・倍率なのか見抜く
6 あとは、「足し算」「引き算」「掛け算」「割り算」で答えを出す
7 「何年後」の場合は〔そろえた頭の)左に伸ばす
8 「何年前」の場合は〔そろえた頭を)縮める
問題)49歳と9歳の親子の年齢差が3倍になるのは何年後ですか?
であれば、「年齢差」部分が、3倍-1倍なので2倍に相当するという
事を見抜くのが大事です。
40歳=2倍ですので、1倍=20歳です。
ですから、求めるべき「何年後」は、
1倍(20)-9=11で、
答えは11年後
という事になります。

線分図を書きます(小学校4年生が書いたもの)
理屈で頭の中で考えるよりも、実際に線分図を書いて、たくさんの
問題を解くことが上達の一番の近道です。
まとめ
線分図を書くテクニック
1 頭を揃えて書く
2 分かっている数字を正確に書く
3 「差」が分かるようにする:補助線を引く
4 全体の割合・比率・倍率を書き込む
5 「差」が全体の中でどれくらいの割合・比率・倍率なのか見抜く
6 あとは、「足し算」「引き算」「掛け算」「割り算」で答えを出す
7 「何年後」の場合は〔そろえた頭の)左に伸ばす
8 「何年前」の場合は〔そろえた頭を)縮める
解き方の基本(テクニック)を理解(分かったら)したら、量を質に転化
させるために、可能な限り大量に問題を解きましょう。
答えを計算できるように、「割合や倍率」をそろえる事ができて、答えを
完璧に導き出せるようになるまで、100問でも1000問でも解くべきです。
ただし、やり方(テクニック)が分かっていないうちは、簡単な問題で、
仕組み(テクニック)をまずは覚えましょう。
練習問題
問題1)
和が127の3つの数、A/B/Cがある。
BはAの3倍より3大きく、CはAの4倍より4大きいとき、
A/B/Cはそれぞれいくつか?
*線分図は自分で書いてみましょう。
問題2)
広場にハトがいます。5羽飛んでいき、次に8羽飛んでいき、残りは
17羽になりました。はじめ、ハトは何羽いましたか?
問題3)
1700円を太郎君、花子ちゃん、びばりちゃんの3人で分けるのに、
太郎君は花子ちゃんより250円多く、花子ちゃんはびばりちゃんより
40円少なくなるように分けました。
太郎君、花子ちゃん、びばりちゃんはそれぞれいくらずつ持っていますか?
問題4)
兄は330円、弟は60円持っていました。2人とも同じ金額のおこづかいを
もらったら兄の持っているお金は弟の4倍になりました。もらったおこづか
いはいくらになりますか。
問題5)
AとBは同じ金額のお金を持っていました。Aは100円、Bは400円
使ったので、AとBの持っているお金の比は5:2になりました。
はじめに持っていたお金はいくらになりますか。
線分図を書くテクニック
1 頭を揃えて書く
2 分かっている数字を正確に書く
3 「差」が分かるようにする:補助線を引く
4 全体の割合・比率・倍率を書き込む
5 「差」が全体の中でどれくらいの割合・比率・倍率なのか見抜く
6 あとは、「足し算」「引き算」「掛け算」「割り算」で答えを出す
7 「何年後」の場合は〔そろえた頭の)左に伸ばす
8 「何年前」の場合は〔そろえた頭を)縮める

こういうものです(筆者撮影・小学校4年生の子供が書いたもの)
問題6)
150枚のカードを岩宿さん、三内丸山さん、吉野ヶ里さんで分けたら、
三内丸山さんは岩宿さんの3/5より12枚多く、吉野ヶ里さんは三内丸山さん
の5/6より2枚多くなりました。それぞれ何枚持っていますか?