約数とは?
約数とはある数を割り切れる整数
(割り切れる→割ったときに余りが「0」になる整数)
の事です。全ての数字を割り切れる「1」やその整数自体も
入ります。
4の約数は「1、2、4」です。
9の約数は「1、3、9」です。
12の約数は「1,2,3,4,6,12」です。
1から順番に割っていっても良いですが、
「100の約数を全て答えなさい」
と言われると、素直にやると考えたらそれだけでなえてしまいますよね?
下記で解説しますが、最終的には
「素数」について覚えて、その上で「素因数分解」で求める
事ができるようにしましょう。小学生でも何度か
読めば、理解は可能だと思います。
「素数」についてはこちら。
まずは基本的な解き方から。
約数の効率的な求め方―中学受験(小学生向け)
2つずつ組にして求める
約数の効率的な求め方はいくつかありますが、一つは
2つずつ組にして求める
です。

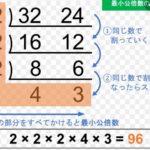
画像出典:https://sugaku.fun/divisor/
このようなイメージです。
原始的ですが、まずはこのやり方で100以下位の数字の約数は
正確に出せるようにしましょう。
例えば「80の約数」なら、
1⇔80
2⇔40
4⇔20
5⇔16
8⇔10
1, 2, 4, 5, 8, 10, 16, 20, 40, 80 答え 10個
80を割れる数字で小さいものから割っていくわけですね。
ただ、これだと数字が大きくなったりすると大変ですね・・・。
「素因数分解」
というテクニックを使うと、大きい数字の約数の数も簡単に
求められます。
約数の(数)の求め方:素因数分解
約数の数・個数を求める場合は「素因数分解」が便利です。
素因数分解=素数だけのかけ算にすること
(例:30→2×3×5)
「約数の数を求めなさい」という問題は中学受験の
算数の問題ではよくあります。
1)素数で割っていく
2)出てきた素数の数にプラス1をしてそれぞれを掛ける
3)(例えば18)3×3×2なら、「3」は2個なので、「2+1」、
「2」は1個なので「1+1」→3×2=6
18の場合。
2)18
3)9
3)3
1
(なぜ出てきた素数の数にプラス1をするのかは数学的理由が
あるのですが、このブログは小学生向けなので省きます)
この公式のポイントは、
「同じ数字の素数の数+1」を掛ける
という部分です。
何度か練習をすれば、おそらくできるようになります。
「素因数分解」をできるようになる順序は、
1)「素数」を覚える
2)「素因数分解」を何度もやる
基本はこの二点でいけるはずです。
約数の(数)の求め方:素因数分解の練習問題
さっそく練習しましょう。上記で原始的に解いた「80」。
素因数分解のやり方
1)素数で割っていく
2)出てきた素数の数にプラス1をしてそれぞれを掛ける
3)(例えば18)3×3×2なら、「3」は2個なので、「2+1」、
「2」は1個なので「1+1」→3×2=6
例題)80の約数の数は?
●素数で割っていく
2)80
2)40
2)20
2)10
5)5
1
●出てきた素数の数にプラス1をしてそれぞれを掛ける
「2が4つ」と「5がつ1つ」ですね?
「4+1」×「1+1」=5×2=10
答え)80の約数の数は10個
どうでしょう、できそうですか?
ポイントは二つだけです。
1)素数で割っていく
2)出てきた素数の数にプラス1をしてそれぞれを掛ける
「素数」を知っていれば基本的にはできるはずです。
例題)100の約数の数は?
2)100
2)50
5)25
5)5
1
(2が2個、5が2個)
(2+1)×(2+1)=3×3=9
答え)9個
どうでしょう、できそうですか?
ポイントは二つだけです。
1)素数で割っていく
2)出てきた素数の数にプラス1をしてそれぞれを掛ける
「素数」を知っていれば基本的にはできるはずです。
例題)48の約数の数は?
例題)99の約数の数は?
例題)222の約数の数は?
ポイントは二つだけです。
1)素数で割っていく
2)出てきた素数の数にプラス1をしてそれぞれを掛ける
「素数」を知っていれば基本的にはできるはずです。
「素数」についてはこちら。
やり方を覚えて、正確にできるようになったら、多数の問題を解いて
いきましょう。数字を入れれば約数の数が瞬時に出るサイトがあり
ますので、練習してみてください。
素因数分解で約数の数(個数)だけでなく・個々の約数も求められる
もちろん、上記の「素因数分解」の方法で、約数の数(個数)だけでなく、
個々の約数を求める事もできます。分解していった素数や約数の掛け算を
すれば、全ての約数が求められます。
例えば、
2)100
2)50
5)25
5)5
1
(2+1)×(2+1)=3×3=9 約数の数(個数)は9個です。
上記の数字を見て、
「1」「2」「5」「25」「50」「100」の6個の約数は
すぐに分かりますね?それ以外は個々の約数をかけて、100未満
のものが100の約数になります。
2×2=4 2×5=10 4×5=20
この3つの約数がそれ以外の100の約数という事になります。
小学生でも慣れればそれほど難しくはないかと思われますので
頑張ってマスターしましょう。
まとめ
以上、
約数の求め方/素因数分解は小学生でもできる!―塾なしで中学受験をする勉強法
でした。
約数を全て求めるには、
2つずつ組にして求める
のが基本となります。

画像出典:https://sugaku.fun/divisor/
ただし、このやり方だと時間がかかるのと、数字が大きくなると難しいです。
そこで「素因数分解」を使って約数の数(個数)や約数を求める事が
できます。
ポイントは、
1)素数で割っていく
2)出てきた素数の数にプラス1をしてそれぞれを掛ける
でしたね?詳細は上記をどうぞ。
(関連記事)