最大公約数とは?
最大公約数は、
いくつかの数の共通の約数のうち最大の数
です。

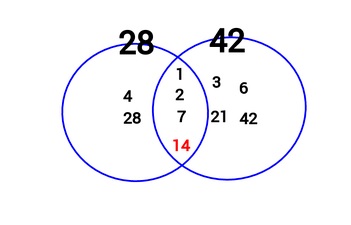
28と42であれば、上記のように、
共通の約数(公約数)が「1、2、7、14」と4つあり、
最大の公約数は14ですので、
28と42の最大公約数は14です。
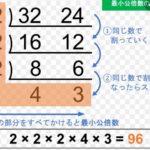
最大公約数の求め方:すだれ算
最大公約数の求め方はいくつかありますが、中学受験(小学生がやる)の
場合「すだれ算」が基本となります。
上記の「28と42の最大公約数」をすだれ算で求めると以下のようになります。
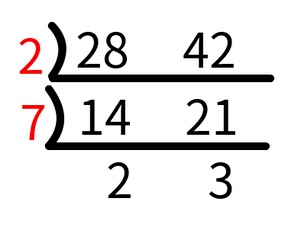
「すだれ算」のやり方
1 最大公約数を求めたい数を横に並べて書く
2 共通して割り切ることができる数を見つける(最小のもの)
3 わり算の筆算を逆向きに書いて割れる数がなくなるまで割る
4 共通して割れるものが1だけになったら終了
5 左側の割った数を全てかけた数字が最大公約数
28と42であれば、2×7=14ですね。
シンプルなものなので、何度か練習すれば習得できるでしょう。
ちなみに数字が3つ以上になっても、仕組み(やり方)は同じです。
例)16 24 40の最大公約数
2}16 24 40
2}8 12 20
2}4 6 10
2 3 5
2×2×2=8
最大公約数の求め方―練習問題
例題)「4と12の最大公約数は?」
2}4 12
2}2 6
1 3
2×2=4 最大公約数は4
例題)「24と36の最大公約数は?」
例題)「36と99の最大公約数は?」
例題)「78と112の最大公約数は?」
例題)「100と108の最大公約数は?」
例題)「48と72と96の最大公約数は?」
2}48 72 96
2}24 36 48
2}12 18 24
3}6 9 12
2×2×2×3=24 答え24
例題)「60と72と96の最大公約数は?」
最大公約数の求め方:ユークリッド互助法
なお「すだれ算」以外に「ユークリッド互助法」という方法があります。
これは数字が大きい場合に使えます。中学受験の場合、難関校以外では
「すだれ算」の方が早いですが、知っておいても良いかもしれません。
ユークリッド互助法の使い方
1 最大公約数を求めたい2つの数のうち、大きい数を小さい数で割る
2 割って出てきたあまりで「1」の計算で割る数だった数を割られる数として割る
3 そのあまりで「2」の計算で割る数だった数を割られる数として割る
4 「3」をあまりが出なくなるまで繰り返す
5 最後の計算の割る数が求める最大公約数である
まあ、図で見ないと分からないですね・・・。
よっぽど数字が大きくなければ「すだれ算」で良いかと思います。
公約数は最大公約数の約数
日本語がわかりづらいですが・・・「公約数は、最大公約数の約数」です。

「28と42」であれば、最大公約数は14ですね?
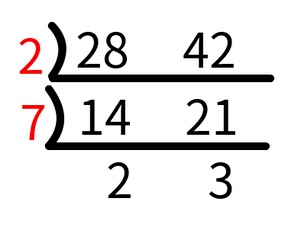

「公約数は、最大公約数の約数」なので、14の約数が28と42の
公約数になります。なっていますね?そういうルールなので絶対に
そうなります。
最大公約数は算数の中学入試の問題では、色々な場面で「使う」
事になるので、本質的に理解して、体で覚えておくのが良いでしょう。
まとめ
算数の場合、
「やり方を覚えたら、正確な方法でひたすらたくさん問題を解く」
というのが、結果としてもっとも効率的な勉強方法ですので、
最大公約数に関しても、ドンドン問題を解きましょう。
量をこなすと質に転化する瞬間があります。
コツとしては、基本問題を徹底してやって、それが完璧になったら
応用問題(最大公約数なら3つ以上の数とか、文章題とか)にうつる
のが良いでしょう。少しずつハードルを上げていくイメージです。
大事なのは、「解き方があっているかどうか」です。答えにいたる
プロセスが正確なら、算数の答えは絶対に正解になります。
数字を入れれば最大公約数を出してくれるサイトを紹介
しますので、数字は自分で適当に入れて100回くらい練習
しましょう。
複数の数字から最大公約数を100%正確に出せるようになったら、
最大公約数を使った文章題などを解いていく必要があります。