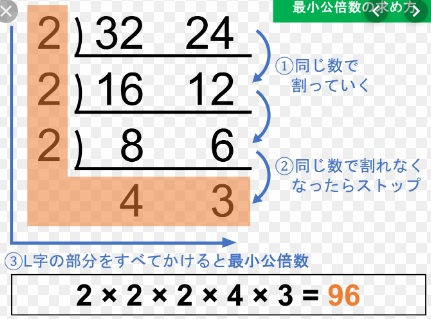
最小公倍数とは
2つ以上の数字の倍数で共通のもので最も小さい数
2と3なら6。
3と7なら21。
1と2と3なら6。
「倍数」が怪しいという方はこちらを先にどうぞ。
最小公倍数の求め方はすだれ算
最小公倍数の求め方は「すだれ算」というものを使います。
下記に本質的な考え方を紹介していますが、中学受験(小学生がやる)
の場合「すだれ算」が基本となります。

この図に書いてあるとおりです。
「すだれ算」のやり方
1 最小公倍数を求めたい数を横に並べて書く
2 共通して割り切ることができる数を見つける
3 わり算の筆算を逆向きに書いて割れる数がなくなるまで割る
4 共通して割れるものがなくなったら、割った数字と残った数字を全て掛ける
「6と12」であれば下記のようになります。
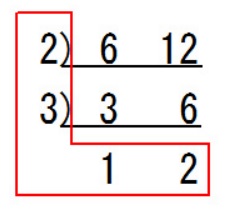
2×3×1×2=12 「6と12の最小公倍数は12」です。
最小公倍数の求め方は数字が3つ以上になっても同じです。
「3と8と9」
3)3 8 9
1 8 3
3×1×8×3=8×9=72
「8 10 12」
2)8 10 12
2)4 5 6
2 5 3
2×2×2×5×3=8×5×3=40×3=120
「すだれ算」のやり方が分かったら、たくさん問題を解いていき
ましょう。こちらのサイトで数字を入れれば最小公倍数が一瞬で
でますので、自分で数字を作ってどんどん練習しましょう。
最小公倍数の求め方としては、基本的には「すだれ算」がもっとも
シンプルでもっとも間違えにくいと思いますが、念のため、本質的な
解き方(考え方)も下記に書いておきます。興味のある方はどうぞ。
(考え方はすだれ算と同じなんですけどね)
最小公倍数の求め方―小学生向けの本質的考え方
1 それぞれの数をそれ以上割れない約数の掛け算であらわす
2 それぞれに共通していない数字(共通させるのに足りないパーツ)をかける
お互いに数字を作っている一番小さいパーツに分けてみると、
お互いを共通させるのに足りないパーツがわかる
例)4と9の最小公倍数は36
1)約数の掛け算で表す
4=2×2
9=3×3
2)それぞれに共通していない数字をかける
4は3×3がないので「2×2×3×3」=36
9は2×2がないので「3×3×2×2」=36
小学生の最小公倍数の求め方では難しい数字は導けない
小学校5年生で習う「最小公倍数」。
公立の小学校で習う「最小公倍数の求め方」は、
個々の倍数を書いていって、共通する数字(最小公倍数)を見つける
という原始的な方法。
(「すだれ算」を習うならそれでやるのが早いですし正確です)
「2と3」の最小公倍数は「6」
2の倍数 2 4 6 8 10
3の倍数 3 6 9 12
「4と9」の最小公倍数は「36」
4の倍数 4 8 12 16 20 24 28 32 36
9の倍数 9 18 27 36
このやり方だと、数字が大きくなったり、3つ以上の数字の最小公倍数
を求めるのが大変(基本的に無理)になる。
大きい数字や3つ以上の数字の最小公倍数の求め方:素因数分解風にすれば
例えば、「7と12の最小公倍数」となっただけで、順番に掛け算を
していくのは骨が折れる。
素因数分解的にすれば、「共通で割れる数字で割れるだけ割って、
後は、残った数字を全てかける」と言えるが・・・。
7と12は共通で割れる数字がないので、7×12=84
3つ以上の数字の場合、
1 共通して割れる一番小さい数字で徹底して割る
2 割り切れない数はしたにそのまま降ろす(下の数字だと、123、123、41)
3 最後に、割った数(下の数字だと2,2,2,3,41)と一番下の横の数字(1,1,1)を全てかける
例えば「24と246と328の最小公倍数」
2 ) 24 246 328
2 ) 12 123 164
2 ) 6 123 82
3 ) 3 123 41
41 ) 1 41 41
1 1 1
2 × 2 × 2 × 3 × 41 × 1 × 1 × 1 = 984
となるが、なかなかそれは・・・。
8と12であれば、
2 ) 8 12
2)4 6
2 3
2×2×2×3=24
上記はほとんど中学生向けなので、小学生向けの最小公倍数の求め方を。
最小公倍数の求め方―小学生向けの本質的な考え方
1 それぞれの数をそれ以上割れない約数の掛け算であらわす
2 それぞれに共通していない数字(共通させるのに足りないパーツ)をかける
お互いに数字を作っている一番小さいパーツに分けてみると、
お互いを共通させるのに足りないパーツがわかる
4と9の最小公倍数は36
1)約数の掛け算で表す
4=2×2
9=3×3
2)それぞれに共通していない数字をかける
4は3×3がないので「2×2×3×3」=36
9は2×2がないので「3×3×2×2」=36
5と6の最小公倍数は30
1)約数の掛け算で表す
5=1×5
6=2×3
2)それぞれに共通していない数字をかける
5は1×5×2×3=30
6は2×3×1×5=30
2と6と9の最小公倍数は18
1)約数の掛け算で表す
2=1×2
6= 2×3
9= 3×3
2)それぞれに共通していない数字をかける
2は1×2×3×3=18
6は2×3×1×3=18
9は3×3×1×2=18
お互いに数字を作っている一番小さいパーツに分けてみると、
お互いを共通させるのに足りないパーツがわかる
8と14の最小公倍数は
8=2×2×2
14=2×7
8は2×2×2×7=56
14は2×7×2×2=56
12と27の最小公倍数は?
12=2×2×3
27=3×3×3
12は2×2×3×3×3=108
27は3×3×3×2×2=108
お互いに数字を作っている一番小さいパーツに分けてみると、
お互いを共通させるのに足りないパーツがわかる
問題 27と36の最小公倍数は
問題 33と42の最小公倍数は