割合=比べられる量÷もとにする量
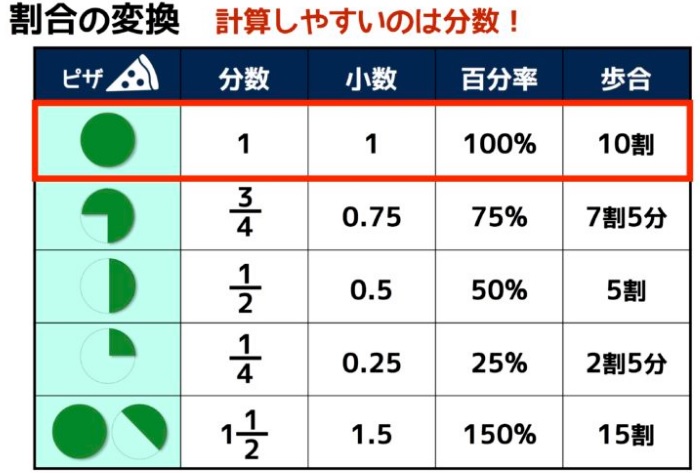
●割合:基準(もとになる量)を1とした時に、比べられる量がどのくらいかを表す
(割合は「分数」「小数」「パーセント(百分率)」「歩合(何割)」で表せる)
例)50(比べられる量)は100(もとにする量)の何パーセントですか?
50÷100=05=1/2=50%
割合は慣れるまでは大変ですが、中学受験に限らず、大人になってからの
日常生活でも「何割引き!」とか「20%オフ!」とか、頻繁に出てきます
ので、ある意味とても実用的なものです。
例)「タイ1匹が1000円の25%オフ!タイ一匹はいくらですか?」
→「25%オフ」=1000円×25%(=0.25)
→250円(値引き分)
→1000円-250円=750円 答え750円
中学受験の算数は、色々なタイプの問題を解けるようになる必要が
ありますが、その前提となるものとして、
●基本的な数字(少数・分数・割合・歩合)●
があります。これは、頭で分かるレベルではなく、体で覚える、
条件反射的に出てくるようになる必要があります。
ポイントは、
「整数:分数:小数:パーセント(百分率):歩合(割合)」
がすぐに結びつく事です。
算数の基本となる数字・割合の基本
まずは、
割合は「分数」「小数」「パーセント(百分率)」「歩合(何割)」で表す(せる)
という事を頭に叩き込みましょう。
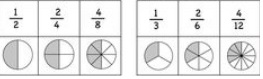
1/2=0.5=50%=5割
1/4=0.25=25%=2割5分
1/5=0.2=20%=2割
(ここまでは「絶対必須」レベルです)
3/4=0.75=75%=7割5分
2/5=0.4=40%=4割
1/8=0.125=12.5%=1割2部5厘
最初は「図」をイメージすると良いと思います。

「少数」や「分数」で見た時は、全体が「1」で、パーセント(百分率)で
見た時は全体が「100%」で、歩合で見た時は、全体が「10割」という事
(ルール)が頭に入り、体で覚え、スラスラと相互に移行できるようになれば
大丈夫です。
それまでは、何度も繰り返し覚えていくのが良いでしょう。
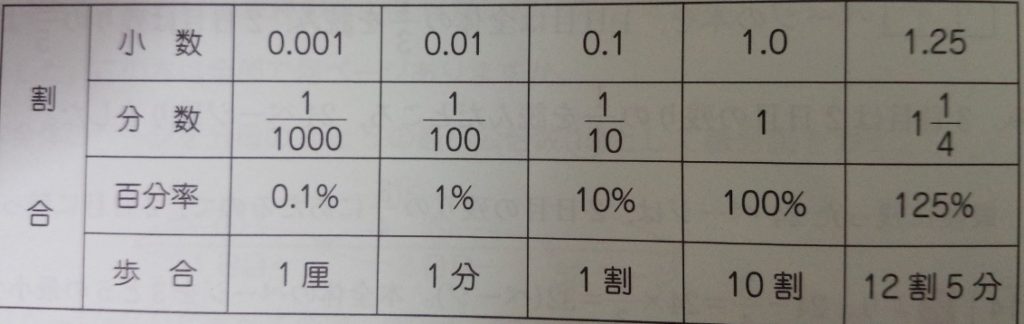
百分率(パーセント・%)
「もとにする量を100としたとき、それに対していくつになるかを
%を用いてあらわしたもの」
歩合
もとにする量の10%(0.1)を1割、1%(0.01)を1分、0.1%(0.001)を1厘
と表す。日本独特の割合の表し方
例)100回打席に立って30回ヒットを打ったら打率は何割?
→30%なので、3割
ポイントは「図を書き簡単に」+「10」や「100」にしてみる
いまいち「完璧」に理解できない場合、以下の2点を意識すると良いです。
1 図を書き、簡単に考える
2 「10」や「100」に直す癖をつける
1 簡単に考える
仮に
3/4=0.75=75%=7割5分
がイメージできない場合、

図を描いてみて、「3/4は1/4が三つ」だなというのを具体的にイメージ
するのが良いでしょう。
もっといえば、
「1/4は1/2の半分だから、0.5÷2で0.25or 50%の半分だから25%」
「0.25が3つだから、0.25+0.25+0.25=0.75or25%が3つだから75%」
くらいまで噛み砕いても良いと思います。
もう一つのポイントは、
2 「10」や「100」に直す癖をつける
2/5=0.4=40%=4割
これも最初はイメージしづらいかもしれません。
ただ、「10」や「100」という単位に直すと、小学生にも
分かりやすくなります。
「2/5=4/10だから40%だな」
という感じです。もちろん、この場合は、2/5=4/10がすんなりと
できないといけないわけですが・・・。
ただ、この「10」や「100」にして考えるという方法は小学生には
かなり有効です。理解がしやすいのでしょう。
1/10=10/100=10%=0.1
2/5=4/10=40%=0.4
3/5=6/10=60%=0.6
1/25=4/100=4%=0.04
「25=100の四分の一=25%」
これは非常に良く出てくる基準になります。
もう一つは、「自分が良く知っている数字で考える」と理解は早いです。
2/5=0.4=40%=4割
であれば、野球少年なら「4割打者」をイメージすれば良いですね。
「5回の打席で2回ヒットで4割打者」
「10打席で4回か!」
という感じです。ちなみに、「4割打者」は超がつく好打者です。
イチローもプロ生活で年間打率4割はなかったです。
野球の世界では「3割打者」が好打者の基準です。
3/10=3割
ですね。
上記の考え方・簡単にする方法を知っていると、「10」や「100」に
簡単に直せない数字でも応用ができます。
例えば、
1/8=0.125=12.5%=1割2部5厘
ですが、いきなりだとイメージしづらくても、「簡単に」考えて、
「1/8=1/4の半分」だなとイメージできれば、1/4が完璧に頭に
入っていれば、
1/4=0.25=25%=2割5分
↓ ↓
1/8=0.125=12.5%=1割2部5厘
とできるものです。
もっと根本的にやりたければ、1/2からやれば大丈夫です。
1/2=0.5=50%=5割
↓ ↓
1/4=0.25=25%=2割5分
↓ ↓
1/8=0.125=12.5%=1割2部5厘
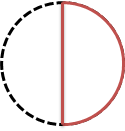
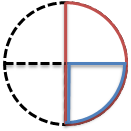
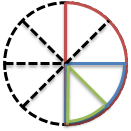
もちろんこのように図に描いてみるのもいいでしょう。
最初のうちはスピードは気にせずに、完璧に理解する事が大事です。
まとめ
以上、
算数の基本となる数字・割合―「中学受験+塾なし」の勉強法!
でした。
中学受験問題を解いていく前に、まずは基本となる、数字・割合を
体で覚えておくというのはとても大事な事です。
いわば、バッティング練習の前にバットを持って素振りを繰り返す
ようなイメージかもしれません。
1/2=0.5=50%=5割
1/4=0.25=25%=2割5分
1/5=0.2=20%=2割
(ここまでは「絶対必須」レベルです)
3/4=0.75=75%=7割5分
2/5=0.4=40%=4割
1/8=0.125=12.5%=1割2部5厘
実際に中学入試の算数の問題を解いていくためには、もっと
多くの数字・割合の置換ができる必要がありますが、上記の
ものは「基本・必須」ですので、体で覚えて一生忘れないくら
いにしておきましょう。