(例題)AがBの75%のとき、A:Bを最も簡単な整数の比で表しなさい。
この問題が、すんなり最後に理解できるようになりましょう。
途中で解説しますので今はわからなくても良いです。
下記の問題も分からなければ「答えを開いて」、解き方を理解し、
何度も解いてみてください。「量をこなして質に転化させる」
事が大事です。
割合―中学受験
■割合=比べられる量÷もとにする量
■割合にあたる量÷1にあたる量
■1にあたる量=割合にあたる量÷割合
(例えば、100人が10%なら、1%は100÷10で10。同様に
128人が32%なら、1%は128÷32で4)
●割合:基準(もとになる量)を1とした時に、比べられる量がどのくらいかを表す
(割合は「分数」「小数」「パーセント(百分率)」「歩合(何割)」で表せる)
例)50(比べられる量)は100(もとにする量)の何パーセントですか?
50÷100=05=1/2=50%
●割合は2つのものの大きさを「~倍」で表した数量
●簡単な数字に置き換えて考える
●ポイントは小数に直してから「倍」をつける
●線分図を書く場合「1」を正確につくり、他を「1」との比較で見ていく
くらべる量=もとにする量×割合
もとにする量=くらべる量÷割合
割合=くらべる量÷もとにする量
割合は慣れるまでは大変ですが、中学受験に限らず、大人になってからの
日常生活でも「何割引き!」とか「20%オフ!」とか、頻繁に出てきます
ので、ある意味とても実用的なものです。
ポイントは、
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
●割合は2つのものの大きさを「~倍」で表した数量
●簡単な数字に置き換えて考える
●ポイントは小数に直してから「倍」をつける
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
あとは慣れる事でしょう。問題をたくさん解きましょう。
(関連記事)
割合の求め方の基本のおさらい
まずは、
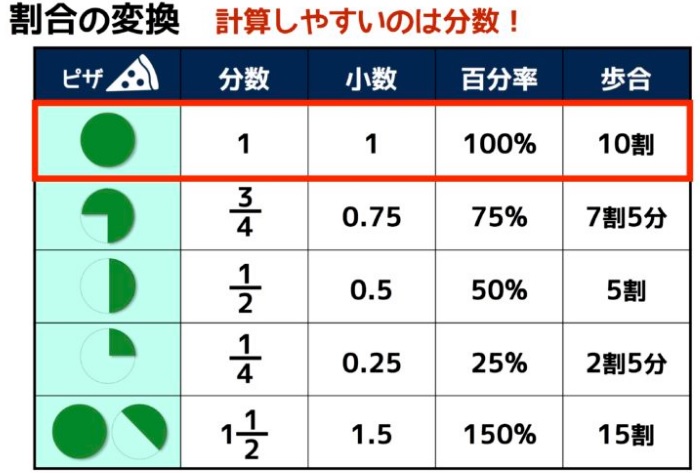
割合は「分数」「小数」「パーセント(百分率)」「歩合(何割)」で表す(せる)
という事を頭に叩き込みましょう。
1/2=0.5=50%=5割
1/4=0.25=25%=2割5分
1/5=0.2=20%=2割
(ここまでは「絶対必須」レベルです)
3/4=0.75=75%=7割5分
2/5=0.4=40%=4割
1/8=0.125=12.5%=1割2部5厘
最初は「図」をイメージすると良いと思います。
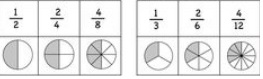
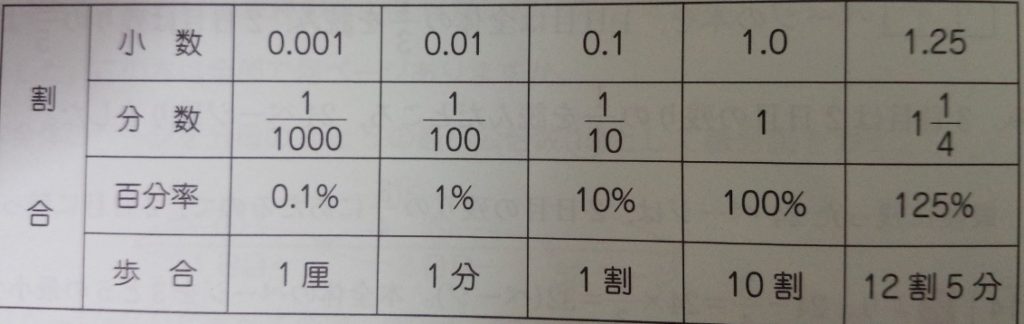
「少数」や「分数」で見た時は、全体が「1」で、パーセント(百分率)で
見た時は全体が「100%」で、歩合で見た時は、全体が「10割」という事
(ルール)が頭に入り、体で覚え、スラスラと相互に移行できるようになれば
大丈夫です。
では、ここで冒頭の問題を考えてみましょう。
(例題)AがBの75%のとき、A:Bを最も簡単な整数の比で表しなさい。
1)「AがBの75%」→【AはBの「3/4」で「7割5分」で(基準1に対して)「0.75」】はOKですか?
2)「AがBの75%」→元になる量は「B」という所もOKですか?
3)という事は、「B」が「基準1」「100%」ですね?
4)A:B=75%:100%、0.75:1、3/4
割合の問題・例題
●割合は2つのものの大きさを「~倍」で表した数量
●簡単な数字に置き換えて考える
●ポイントは小数に直してから「倍」をつける
問題)
びばりさんが持っていたお金の85%を使ったら、残ったお金は450円でした。
はじめにびばりさんが持っていたお金はいくらですか?
問題)30人は120人の何%ですか?
簡単に考えるのが大事です。
10人は100人の何%か?なら分かりますよね?
10÷100=0.1(倍)=10%
この式の数字を入れ替えるだけです。
10人が100人の0.1倍(10%、1/10)であるのと同様に、
30人は120人の0.25倍(25%、1/4)という事です。
もし、上記の問題がまだ「よく分からない」という場合は、下記の基本記事を
再度よく読んでください。
~~~~~~~~~~~~~~~~~~~~~~~~~
●割合は2つのものの大きさを「~倍」で表した数量
●簡単な数字に置き換えて考える
●ポイントは小数に直してから「倍」をつける
~~~~~~~~~~~~~~~~~~~~~~~~~

問題)560円は700円の何割にあたりますか?
単純に考えてください。500円は1000円の何割?
なら簡単ですよね?
500÷1000=0.5(倍) 50%なので5割です。
問題)びばりさんのクラスの全生徒は25人。今日は2人欠席。今日の出席率は何%?
シンプルに考えてください。全生徒100人で3人欠席なら、97人いるので、
出席率97%ですよね?97÷100=0.97(倍)、97%
~~~~~~~~~~~~~~~~~~~~~~~~~
●割合は2つのものの大きさを「~倍」で表した数量
●簡単な数字に置き換えて考える
●ポイントは小数に直してから「倍」をつける
~~~~~~~~~~~~~~~~~~~~~~~~~
問題)500円のマスクが600円に値上げされました。何%値上げされましたか?
600円が500円の何倍かを%で出せば良いわけです。
1/2=0.5=50%=5割
1/4=0.25=25%=2割5分
1/5=0.2=20%=2割
(ここまでは「絶対必須」レベルです)
3/4=0.75=75%=7割5分
2/5=0.4=40%=4割
1/8=0.125=12.5%=1割2部5厘
問題)原価の4割増しの定価をつけましたが、売れないので、
定価の2割引きで売りました。実際に売った値段は原価の何倍ですか?
こういう問題はとにかく、簡単な数字に置き換える事です。
割合でよく使われるテクニック・コツ(小数に直してから「倍」+「1」で揃えて線分図を書く)
~の□%増→(100+□)% ~の□%減→(100-□)%
~の□割増→(10+□)割 ~の□割減→(10+□)割
●割合の問題のポイント/コツは小数に直してから「倍」をつける
例題)
A市の昨年の人口は一昨年より5%減って、13300人でした。今年の
人口は昨年の人口より2割増加しました。一昨年の人口および今年の
人口はそれぞれ何人ですか?
「全体の20%」「残りの3分の一」のように「1」にあたる量が
変わっていく場合、は「1」にあたる量の種類だけで線分図を
書いて条件を整理すると分かりやすくなります。
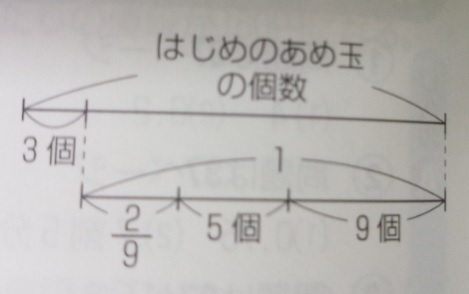
例題)花子さんは箱の中のあめ玉を初めに3個取り、次に残りの2/9より
5個多く取ったら、箱の中に9個残りました。初めに箱の中にあめ玉は何個
ありましたか?
まとめ
割合=比べられる量÷もとにする量
●割合:基準(もとになる量)を1とした時に、比べられる量がどのくらいかを表す
(割合は「分数」「小数」「パーセント(百分率)」「歩合(何割)」で表せる)
例)50(比べられる量)は100(もとにする量)の何パーセントですか?
50÷100=05=1/2=50%
●割合は2つのものの大きさを「~倍」で表した数量
●簡単な数字に置き換えて考える
●ポイントは小数に直してから「倍」をつける
●線分図を書く場合、何を「1」にするかが大事
くらべる量=もとにする量×割合
もとにする量=くらべる量÷割合
割合=くらべる量÷もとにする量
問題が分からなければ「答えを開いて」、解き方を理解し、
何度も解いてみてください。「量をこなして質に転化させる」
事が大事です。