逆算のポイントは「－□」と「÷□」（□が右にある時）・テクニックは3つ―塾なしで中学受験をする勉強法

「計算の順序」がまだ完璧でない場合は先に読んでおいてください。

逆算のポイントとテクニック

 

逆算とは？

中学受験における「逆算」は、

１　数式内の□を求める計算

２　＝の反対側に移動させる計算

方法と考えておけばいいでしょう。

具体的に見るのが一番早いですね。

 

逆算の例題）□＋7＝10　□に当てはまる数字を求めなさい

みたいなものです。□＋7＝10だけなら、見ただけで□＝３と

分かりますが、上に書いたように逆算にはルールがあります。

（□＋５）÷4＝8

のような複雑な問題になると、見ただけでは分かりませんので、

ルール（公式）に沿って解いていく事になります。

 

逆算のルール：＝の反対側に移動させる方法

 

ですので、まずは逆算の基本ルール

「＝（イコール）の反対側に数字を移す時は逆にする」

を理解して、その後、逆算の特殊ルール

「ただし「－□」「÷□」の時はそのまま移動」

を覚えれば良いかと思います。

 

先ほどの問題を解いてみましょう。

（□＋５）÷4＝8　□の数字を求めなさい

（□＋５）÷4＝8

（□＋５）＝8×４

□＋５＝32

□＝32－５

□＝27

 

逆算を解くテクニック：計算の順序を書く＋順序の大きい方から計算する＋大きい□

複雑な逆算を解く際には、以下のテクニックを使いましょう。

１）計算の順序を書く

２）順序の大きい方から計算する（＝の反対側に持っていく）

3）大きい□を意識する

 

　　①　　　②

（□＋５）÷4＝8

②から計算しますので、以下になります。

（□＋５）÷4＝8

ポイントは、このように（□＋5）を大きい□と考える事です。こうすると、

記号は「÷」一つになるので分かりやすいですね？複雑な計算の

逆算になればなるほど、この考え方が大事になります。

（□＋５）＝8×４

□＋５＝32

□＝32－5

□＝27

 

例題）（□＋3）×7＝35　□の数字を求めなさい

　　①　　②

（□＋3）×7＝35

□＋3＝35÷７

□＋3＝5

□＝5－３

□＝2

 

 

例題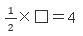）　□の数字を求めなさい

□＝４÷1/2

□＝4×2/1

□＝8

 

例題）543－（17＋□×6）×4＝91

これくらいの計算になると、

１）計算の順序を書く

２）大きい方から計算する（＝の反対側に持っていく）

3）大きい□を意識する

をキッチリとやる必要があります。

１）計算の順序を書く

④　　　②　　①　　③

543－（17＋□×6）×4＝91

２）大きい方から計算する（＝の反対側に持っていく）

3）大きい□を意識する

④　　　②　　①　　③

543－（17＋□×6）×4＝91

　　　↓

（17＋□×6）×4＝543－91

（「－□」「÷□」の時はそのまま移動）

　　　↓

（17＋□×6）×4＝452

          ↓

　②　　①　　③

（17＋□×6）×4＝452

  　　　↓

（17＋□×6）＝452÷４

　　　↓

（17＋□×6）＝113

 　　　↓

　②　　①　　

（17＋□×6）＝113

　　　↓

（17＋□×6）＝113

　　　↓

□×6＝113－17

□×6＝96

□＝96÷6

□＝16

 

逆算の練習問題

（□＋4）×3＝18

 

12×（□－38）＝348

 

85-(234－□×9）＝40

 

6×（89－□÷3）＝372

 

567－（19＋□×７）×4＝183

 

まとめ―逆算のポイントとテクニック

 

「計算の順序」がまだ完璧でない場合は先に読んでおいてください。