画像出典:https://yuzupa.com/tokeizan/
時計算のポイント3つ
1 時計は全体で360度・5分ごとに30度(360÷12)
2 長針は短針に一分間で5.5度追いつく
3 答えは分数等できれいな数字ならなくても良い
例題)3時と4時の間で、時計の長針と短針が重なるのは何時何分ですか?
(解答・解説は下記で)*解き方知らないとできませんよね・・・(大丈夫です、できます)
時計算とは?
時計の長針(1時間に360度・1周)と短針(12時間で360度・1時間で30度)
が作る角度やその他(重なる時とか一直線になる時)を問う問題です。
時計算は、時計の長針と短針を使った「旅人算」と考えられます。
しかも、時計は長針と短針が同じ方向に動きますので、
●二人の進行方向が同じ場合(追いつき算)
→追いつく時間=2人の間の距離÷2人の速さの差
この「旅人算」のテクニックが使えます。
ですので、先に「旅人算」について読んでおいてください。
時計算の解き方・テクニックは「5.5度」!「旅人算」の追いつき算
時計は全体で360度・5分ごとに30度(360÷12)
時計は全体で360度・5分ごとに30度(360÷12)
これは覚えましょう。
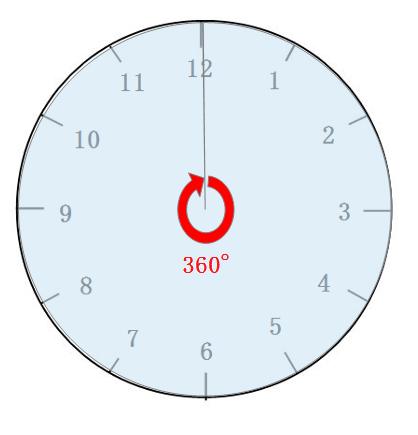
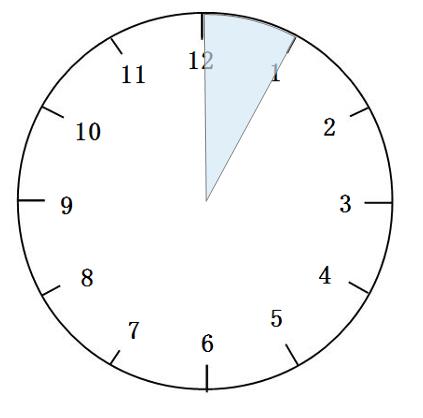
(水色部分が30度)画像出典:https://jukensansuu.com/tokeizan2.html
時計算は、時計の長針と短針を使った「旅人算」と考えられます。
時計は長針と短針が同じ方向に動きますので、
●二人の進行方向が同じ場合(追いつき算)
→追いつく時間=2人の間の距離÷2人の速さの差
この「旅人算」のテクニックが使えます。
となると、ポイントは
1 2つ(長針と短針)の間の距離を考える
2 長針と短針の進むスピード差(1分で5.5度)を知る
という部分になります。
時計算:長針と短針の進むスピード・角度

画像出典:https://yuzupa.com/tokeizan/
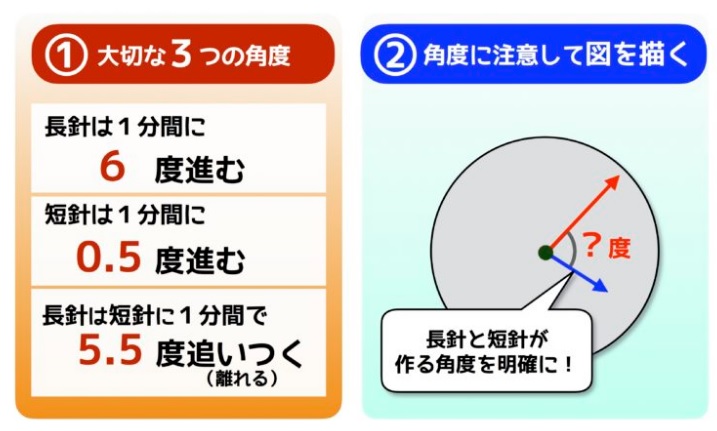
長針:1時間に360度・1分で6度進む
短針:12時間で360度・1時間で30度・1分で0.5度
6-0.5=5.5
長針は短針に一分間で5.5度追いつく
これが時計算の基本中の基本です。覚えてしまった方が良いでしょう。
時計算のポイント3点の再確認です。
1 時計は全体で360度・5分ごとに30度(360÷12)
2 長針は短針に一分間で5.5度追いつく(逆に行く場合は1分間に6.5度〔6+0.5〕)
3 答えは分数等できれいな数字ならなくても良い
冒頭の例題を解いてみましょう。
例題)3時と4時の間で、時計の長針と短針が重なるのは何時何分ですか?
なお、時計の図はある程度きれいに書けた方が良いです。
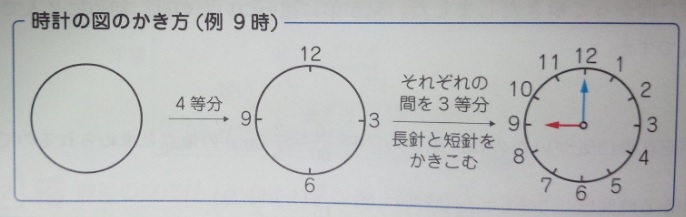
慣れないうちは、上記に加えて、「対角線」も引いてしまったほうが良いです。
(1と7、2と8、3と9、4と10、5と11、6と12)
例題)3時と4時の間で、時計の長針と短針が重なるのは何時何分ですか?
 →
→![時計のスマホ壁紙 検索結果 [10] 画像数9736枚 | 壁紙.com](https://img.kb-cdn.com/imgviewer/NVpIM2ptOHhYRzVmUk5rM1NrNlFxYVV6enV4aGk2UFRJMmxPckdDUUVNWWZ6OEZCem5zdzdnT1B2SkFDZXduUUIwMUR4WW4zdXlaV0s4VFV0R3p5Z0NjbHNhNDRrcTFyMVpJcTNWbW9EcjRpa2RyS04vK0VWU21WV2gvL2tucE1oNHpZT2dQclZieGhXZmVVRVJpeTN6N0VzNjcyMUhMRGlvV29xc1VScHhFV0E0eGJRSWpSSlpZTFNaYnI0WEZLQm5vTVRmaHFlNFJwRnJPYyttU3FOdz09?square=0)
長針は短針に一分間で5.5度追いつく
これが時計算の基本です。
3時の時の長針と短針が作る角度は、30×3=90度
(時計は全体で360度・5分ごとに30度(360÷12))

12と3の間は15分ですしね。
しつこいようですが、
長針は短針に一分間で5.5度追いつく
です。
時計算は、時計の長針と短針を使った「旅人算」と考えられます。
しかも、時計は長針と短針が同じ方向に動きますので、
●二人の進行方向が同じ場合(追いつき算)
→追いつく時間=2人の間の距離(角度)÷2人の速さの差
でしたね?
2人の間の距離=長針と短針の作る角度(90度)
2人の速さの差=1分に5.5度追いつく(短くなる)(5.5度)
90÷5.5=16.36363636~~~(割りきれません・・・)
こういう場合は、分数で答えを出します。
(3 答えは分数等できれいな数字ならなくても良い)
90/5.5=900/55=16と20/55=16と4/11
答え)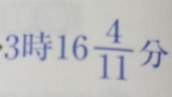
(基本)時計算の問題パターン
1 「時計の長針と短針が重なるのは何時何分ですか?」系
上記の例題のようなものです。これは
1)「2人の間の距離=長針と短針の作る角度」を確認する〔大きい角度と小さい角度があります)
2)「2人の速さの差=1分に5.5度追いつく(短くなる)」
3)1)の角度÷5.5
この解法パターンで基本問題は解けます。
2 「何時何分の時、長針と短針が作る小さい角度は何度ですか?」系
1)(慣れないうちは)時計の時間を書く〔対角線全てに線を引くと良い、1と7、2と8など)
2)時計の数字(123456789101112)の個々の間は30度
3)長針は1分で6度、短針は1分で0.5度動く
4〕ここから計算する
(慣れるまではきちんと時計を書いた方が良いです)
(基本)時計算の中学受験問題等
問題)鎌倉学園中学
長針、短針のある時計が2時20分を示しているとき、長針と短針が
つくる小さい角の大きさは□度です。
この種の問題の解法パターンは、
1)〔慣れないうちは)時計の時間を書く〔対角線全てに線を引くと良い、1と7、2と8など)
2)時計の数字(123456789101112)の個々の間は30度
3)長針は1分で6度、短針は1分で0.5度動く
4〕ここから計算する
でしたね?
問題〕桜美林中学
8時と9時の間で、時計の長針と短針が重なる時間は何時何分ですか。
小数第一位を四捨五入して答えなさい。
この種の問題の解法パターンは、
1)「2人の間の距離=長針と短針の作る角度」を確認する〔大きい角度と小さい角度があります)
2)「2人の速さの差=1分に5.5度追いつく(短くなる)」
3)1)の角度÷5.5
でしたね?
まとめ―(基本)時計算の解き方・テクニックは「5.5度」!「旅人算」の追いつき算!
1 時計は全体で360度・5分ごとに30度(360÷12)
2 長針は短針に一分間で5.5度追いつく
3 答えは分数等できれいな数字ならなくても良い
あとは、問題を多く解いて基本を完璧にしておきましょう。
その上で応用をやっていけばいいと思います。
〔関連記事)
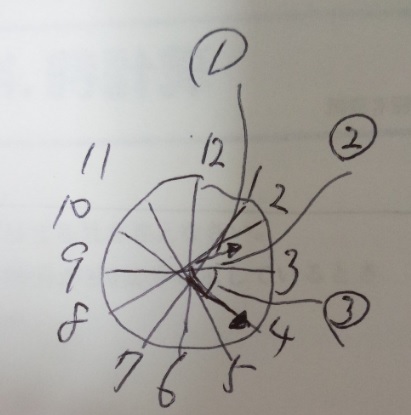 2時20分という事は、短針は「2と3の間の2より」、長針は
2時20分という事は、短針は「2と3の間の2より」、長針は