「容器に入った水に物を入れる」系問題―「中学受験＋塾なし」の勉強法!

（関連記事）

「水の入った柱体（容器）」系の問題

容器から容器に水を移しかえたり、傾ける問題は上記記事でみました。

ここでは、

「容器に入った水に物を入れる」

系の問題を見ていきたいと思います。

ポイントは

●物を入れて上がった水位

●水の量は変わっていない

です。

 

「容器に入った水に物を入れる」系問題

ポイントは

●物を入れて上がった水位

●水の量は変わっていない

です。

また、この「容器に入った水に物を入れる」系の問題では、

▲物がすべて水に入る

▲物がすべては水に入らない（一部上に出ている）

の2パターンがあります。

 

なお、この種の問題は、立体図を書く必要はなく、断面図を書くやり方のほうが

間違いが少ないです。

 

物がすべて水に入るパターン

「物が全て水に入っている」＝物と同じ体積分の水を入れたと考えられる。

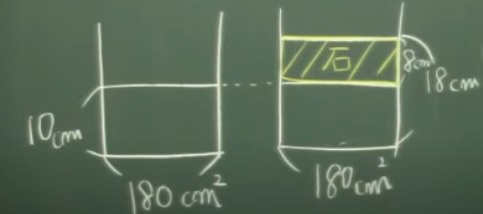
問題）底面積180cm²の水槽には水が10cmの水位まで入っています。

石を入れたら水位が8cm上がりました。石の体積は？

上がった水位＝物の体積÷容器の底面積

物の体積＝容器の底面積×上がった水位

8=物の体積÷180

物の体積＝180×8＝1440

答え）1440cm³

 

問題）1辺20cmの立方体の容器に高さ13cmまで水が入っています。この中に右の

1辺10cmの立方体を全部水の中に入れると、水面の高さは入れる前より□cm高くなります。

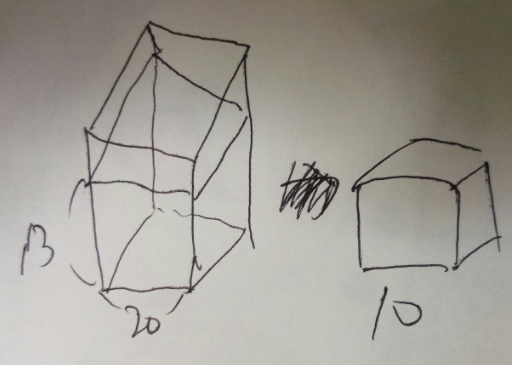
（13cmと20cmの比率…細かい事は気にしない!）

上がった水位＝物の体積÷容器の底面積

物の体積＝容器の底面積×上がった水位

上がった水位＝10×10×10÷400＝1000÷400＝2.5

答え）2.5

 

物がすべては水に入らない（一部上に出ている）パターン

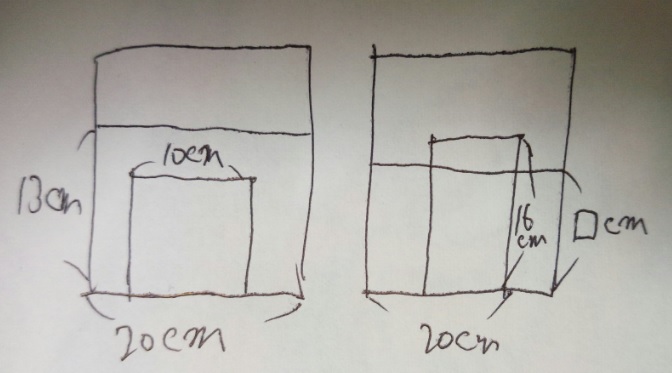
問題）左図は1辺20cmの立方体の容器に、底面が1辺10cmの正方形で

高さが16cmの直方体のおもりが横にして入っています。水位は13cmです。

このおもりを右図のように縦にすると水面は□cmになります。

新たな水位＝水の体積÷新たな底面積（容器の底面積－物の底面積）

物を入れる前後で底面積の比と水位の比は逆比になる

新たな水位＝（（20×20×13）－（10×10×16））÷（20×20－10×10）

　　　　　＝（5200－1600）÷300

　　　　　＝3600÷300＝12

答え）12

 

「容器に入った水に物を入れる」系の中学入試問題等

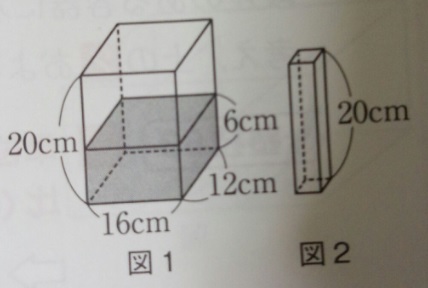
問題）日本女子大付属中学（問題文はワイが少し変えてます）

図2の底面は正方形です。図2を図1に垂直に立てると水位が3cm

上がりました。図2の底面の1辺の長さは何cmですか？

新たな水位＝水の体積÷新たな底面積（容器の底面積－物の底面積）

物を入れる前後で底面積の比と水位の比は逆比になる

どちらを使っても解けます。

物を入れる前後で底面積の比と水位の比は逆比になる

こちらからいきますか。

水位の比→前６（２）：後９（３）　なので底面積の比→前192（③）：後「128」②

後の128は（16×12）－図２の底面積（仮にA×Aとする）

128＝192－A×A　64＝A×A　A=８　答え）8cm

新たな水位＝水の体積÷新たな底面積（容器の底面積－物の底面積）

こちらでも解けます。

9cm＝16×12×６÷（16×12－（図２の底面積（仮にA×Aとする）））

９＝1152÷（192－（A×A））　逆算注意!（「÷□」のパターンです）

128＝（192－（A×A））　逆算注意!（「－□」のパターンです）

64＝A×A　A＝８

答え）8cm

 

問題）立教新座中学（問題文はワイが少し変えてます）

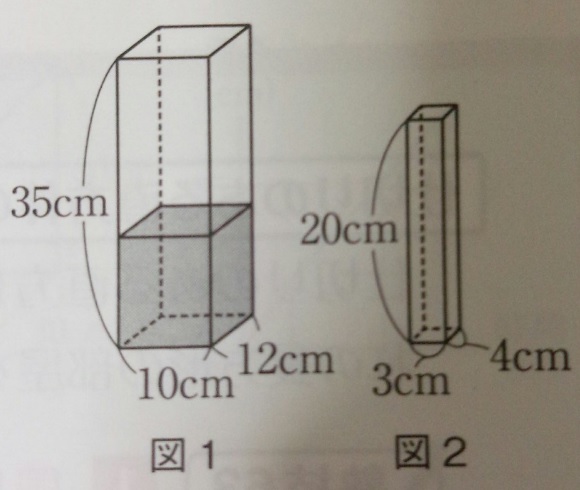
図1に図2の棒をまっすぐ底がつくまで入れます。棒を1本入れた

とき、棒の一部は水面から出ていて水面の高さは1cm高くなり

ました。

（１）初めの水面の高さは？

（２）棒を何本入れると入れた棒全てが完全に水の中に入りますか。

最も少ない本数を答えなさい。

（１）初めの水面の高さは？

物を入れる前後で底面積の比と水位の比は逆比になる

底面積の比120：108→10：9

水位の比9：10　比率１が1cmなので、最初は9cm

（２）棒を何本入れると入れた棒全てが完全に水の中に入りますか。

最も少ない本数を答えなさい。

①水面の高さが20cmになった時が棒が全て水の中に入る

②棒を入れる前と後の水面の比は9：20→底面積の比は20：9

③棒が入っていない時の底面積は120。120：A→20：9　A=54

120-54＝66　入れた棒の面積の合計は66cm²以上

④棒の底面積は12cm²　なので、66÷12＝5.5　5.5本とはできないので、6本以上必要

答え）6本

答え）（１）9cm（２）6本

 

まとめ

ポイントは

●物を入れて上がった水位

●水の量（体積）は変わっていない

です。

（関連記事）

「水の入った柱体（容器）」系の問題