すい体(三角すい・四角すい・円すい)の公式とテクニック!円すいがポイント!
「水の入った柱体(容器)」系の問題もいくつかパターンがあります。
★水を柱体(円柱など)に移しかえて、水位(高さ)を求める
★水の入った容器を傾ける系の問題
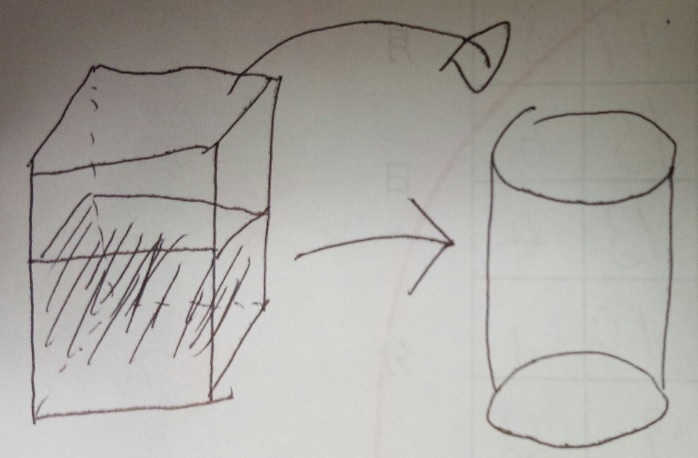
こんなイメージです。
水位=水の体積÷容器の底面積
水の体積=容器の底面積×水位
→水の体積が一定なら、容器の底面積の比と水位の比は逆比になる
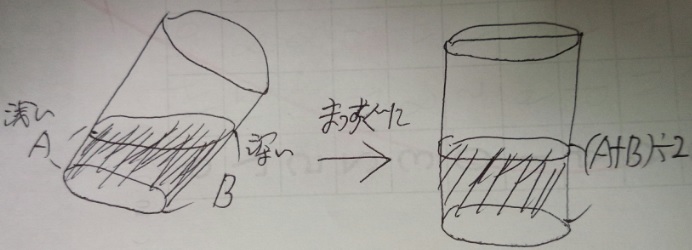
★傾けた時に「上と底」でピタッとなる場合満タンの半分★
★傾けた時の水の高さの真ん中=真っ直ぐにした時の水位★
(深い水位+浅い水位÷2=真っ直ぐの水位)
★容器を傾ける系の問題では、「空洞」部分の体積に注目する★
水を柱体(円柱など)に移しかえて、水位(高さ)を求める系問題
水位=水の体積÷容器の底面積
水の体積=容器の底面積×水位
→水の体積が一定なら、容器の底面積の比と水位の比は逆比になる
問題)左の容器の水の体積が314cm³の場合、右の円柱にすべて
水を移し変えた場合の水位(高さ)は何cmですか?なお、円柱の
半径は5cm、円周率は3.14とします。

水位=水の体積÷容器の底面積
この公式が使えます。
体積314cm³で、円柱の底面積は5×5×3.14=78.5
314÷78.5=4
答え)4cm
水位=水の体積÷容器の底面積
水の体積=容器の底面積×水位
→水の体積が一定なら、容器の底面積の比と水位の比は逆比になる
問題)下図の左は1辺6cmの立方体です。高さ4cmまで水が
入っています。この水を全て右の三角柱に入れます。水面の
高さは何cmになりますか?
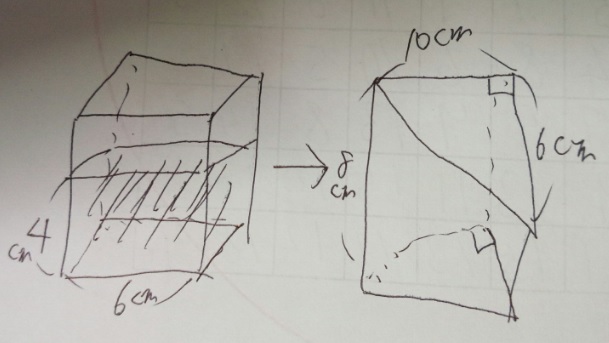
絵が下手ですが、我慢してください。人生我慢も必要です。問題文きちんと読んで。
水の体積=容器の底面積×水位
→水の体積が一定なら、容器の底面積の比と水位の比は逆比になる
1)水の体積=36×4=144cm³
2)水の体積が一定なら、容器の底面積の比と水位の比は逆比になる
(左)底面積36(⑥):(右)30(⑤)→逆比→水位(左)4(⑤):(右)⑥
高さの比が⑥:⑤なので、水位の比は逆比で⑤:⑥になります。
割合⑤が4cmなので、割合⑥は4×6/5=24/5=4.8
答え)4.8cm
水位=水の体積÷容器の底面積
水の体積=容器の底面積×水位
→水の体積が一定なら、容器の底面積の比と水位の比は逆比になる
水の入った容器を傾ける系の問題
★傾けた時に「上と底」でピタッとなる場合満タンの半分★
★傾けた時の水の高さの真ん中=真っ直ぐにした時の水位★
(深い水位+浅い水位÷2=真っ直ぐの水位)
★容器を傾ける系の問題では、「空洞」部分の体積に注目する★

出典:https://jukensansuu.com/katamukeru.html
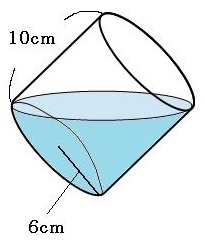
問題)底面の半径が6cm、高さが10cmの円柱の容器に水を入れて、上の図の
ように傾けます。 入っている水の体積は何cm³ですか?円周率は3.14
★傾けた時に「上と底」でピタッとなる場合満タンの半分★
このパターンがこれです。
容器の円柱の容積÷2
6×6×3.14×10÷2=565.2
答え)565.2cm³
★傾けた時の水の高さの真ん中=真っ直ぐにした時の水位★
(深い水位+浅い水位÷2=真っ直ぐの水位)
これは図を見るのが一番でしょう。

これは図を見ると分かりやすいのでは?
問題)入っている水の体積は?
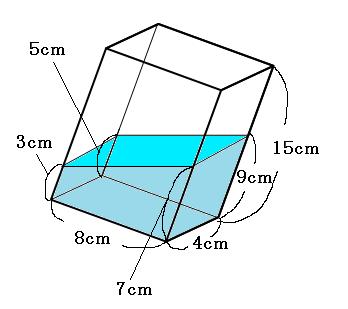
1)見るべき数字は深い部分9cmと浅い部分3cm
2)真っ直ぐにすると、水位は(3+9)÷2=6
3)8×4×6=192
答え)192cm³
★傾けた時の水の高さの真ん中=真っ直ぐにした時の水位★
(深い水位+浅い水位÷2=真っ直ぐの水位)
最後、
★容器を傾ける系の問題では、「空洞」部分の体積に注目する★
問題)聖セシリア女子中学(問題文はワイが変えてます)
左は水でいっぱい、真ん中のように水をこぼし右のように戻しました。Xは何cm?
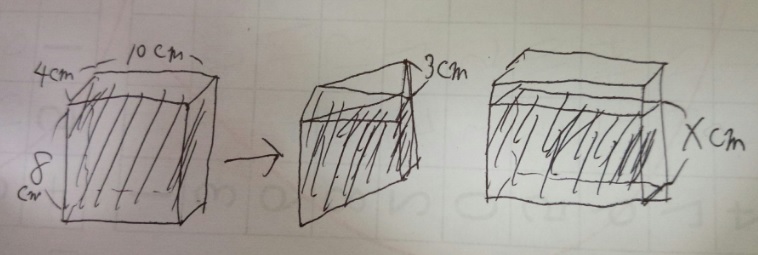
★傾けた時の水の高さの真ん中=真っ直ぐにした時の水位★
(深い水位+浅い水位÷2=真っ直ぐの水位)
こちらでも解けますし、簡単で速いです。
深い水位が8で浅い水位が5なので、13÷2=6.5 答え)6.5cm
★容器を傾ける系の問題では、「空洞」部分の体積に注目する★
こちらで解く場合(面倒ですが)
1)真ん中の空洞は三角柱:3×10÷2×4=60cm³
2)1)を右の底面積で割る:60÷40=1.5
3)右の空洞の高さは1.5なので8-1.5=6.5
★傾けた時に「上と底」でピタッとなる場合満タンの半分★
★傾けた時の水の高さの真ん中=真っ直ぐにした時の水位★
(深い水位+浅い水位÷2=真っ直ぐの水位)
★容器を傾ける系の問題では、「空洞」部分の体積に注目する★
すい体(三角すい・四角すい・円すい)の公式とテクニック!円すいがポイント!