ここでは「加比の理(かひのり)」という考え方を使って三角形の図形問題をやります。
加比の理(かひのり)?????やめて~~~~~ですね?ビビル必要はありません。
その前に、面積比は高さの等しい三角形の組を探す!相似は2乗!①の記事にある、
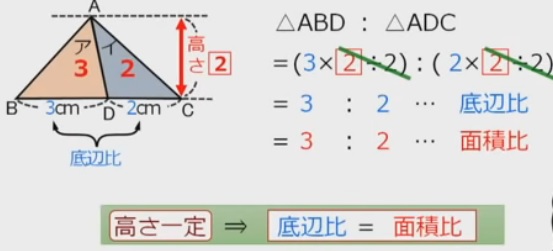
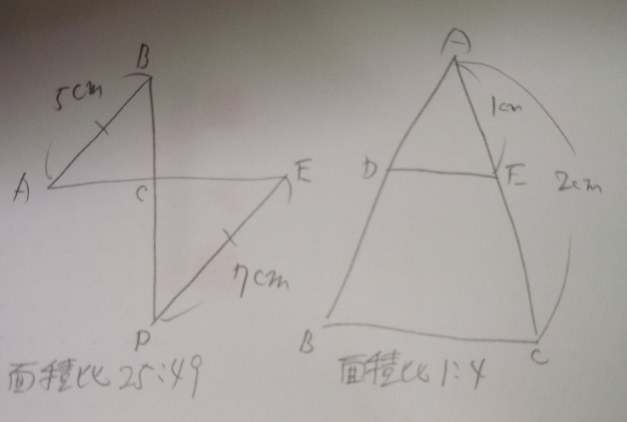
●高さが等しい三角形→底辺比=面積比●
●三角形が相似の場合、面積比は相似比の2乗と同じ●
この点を完璧にしておいてください。
面積比:加比の理(かひのり)の基本
★加比の理(かひのり)★
比率A:Bと比率C:Dが同じである時、
(A+C):(B+D)の比や
(A-C):(B-D)の比はA:Bと同じになる
これ(加比の理)を三角形の図形の問題で理解していくのが基本です。
図形(三角形)の前に、加比の理(かひのり)を文章題で見てみましょう。
「だろう君が2000円(A)、びばりさんが1500円(B)持っています。
二人の所持金の比率は「4」(A):「3」(B)ですね?
ごんた君がやってきて、だろう君に400円(C)、びばりさんに300円(D)
あげたとします。あげたお金の比も④(C):③(D)ですね?」
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
比率A:Bと比率C:Dが同じである時、
(A+C):(B+D)の比や
(A-C):(B-D)の比はA:Bと同じになる
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
比率はA:BもC:Dも、ともに4:3
(A+C):(B+D)→(2000+400):(1500+300)→2400:1800→4:3
(A-C):(B-D)→(2000ー400):(1500ー300)→1600:1200→4:3
★加比の理(かひのり)★
比率A:Bと比率C:Dが同じである時、
(A+C):(B+D)の比や
(A-C):(B-D)の比はA:Bと同じになる
分かりますよね?これを三角形の図形の面積問題に応用していきます。
加比の理(かひのり)と三角形の面積比
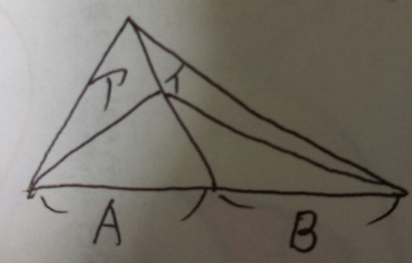
【ア(の面積):イ(の面積)=A:B】
これが基本となります。なぜこの公式が成り立つか分かりますか?
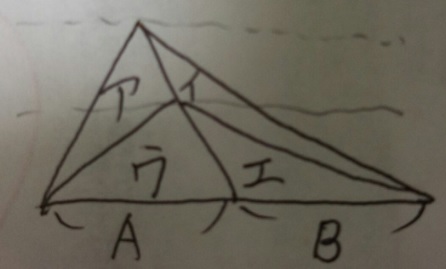

ウの面積:エの面積は高さが同じなので、A:B
という事は、ア+ウ:イ+エもA:B
なので、(ア+ウーウ):(イ+エ-エ)もA:B

【ア(の面積):イ(の面積)=A:B】
これを覚えるのではなく理解してください。
問題)三角形ABCでAF:FC1:1、BE:EC2:1のとき、AD:DBを最も
簡単な整数比で表してください。
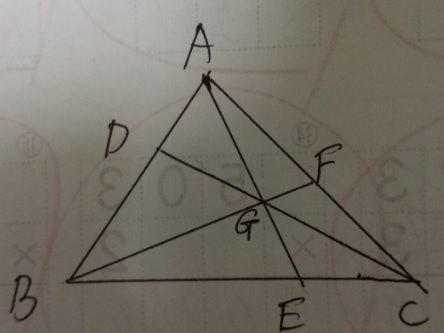
1)分かる要素を書き出す+三角形を分ける(最初はいくつか図を書いた方が良い)
2)加比の理から、三角形AGB:三角形AGCは2:1
同じく、三角形AGBと三角形CGBは①:①、三角形AGBを割合2で揃えると、
三角形AGB「2」:三角形AGC「1」:三角形CGB「2」
3)求めるべきAD:DBは三角形AGC「1」:BGC「2」と同じ比と分かる
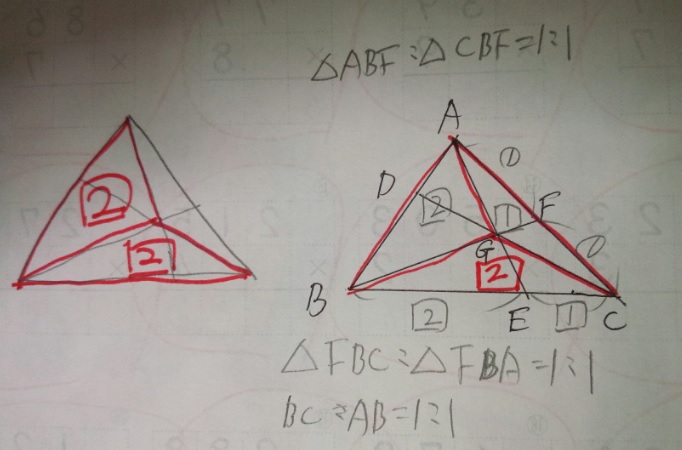
答え)1:2
面積比:加比の理(かひのり)の中学入試問題等
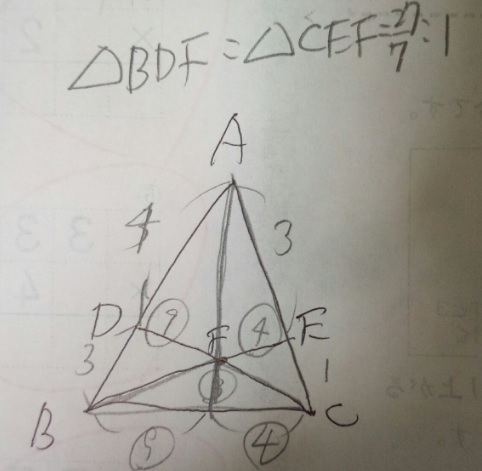
問題)芝中学
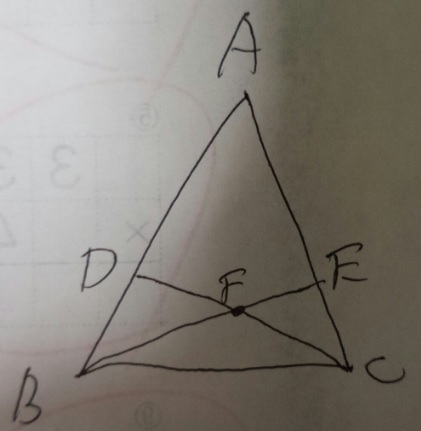
三角形ABCにおいてAD:DB=4:3、AE:EC=3:1」とした時、
三角形BDFと三角形CEFの面積比を最も簡単な整数比で表してください。

1)AFに補助線を引きましょう
2)三角形ABF「3」:三角形BCF「1」
3)三角形ACF④:三角形BCF③
4)連比で揃えられそうです。
ABF「3」:BCF「1」
BCF③: ACF④
なのでBCFを③で揃えましょう(連比は大丈夫?)。
ABF⑨:BCF③:ACF④

5)三角形ECFと三角形ACFは高さが同じなので面積比は底辺比(1:4)と同じ
ACFの面積比は④でしたので、④×1/4で三角形ECFの面積比は①
6)(同じように)三角形BDFと三角形BAFは高さが同じなので面積比は底辺比(3:7)
三角形BDFは三角形BAFの3/7の面積。三角形BAFの面積比は⑨だったので、
三角形BDFの面積比は⑨×3/7で27/7
三角形BDFと三角形CEFの面積比を最も簡単な整数比で表してください。
という問題なので、
27/7:1→27:7
答え)27:7
最初は分からなくてもじっくりと解法を読んで自分で解けるようにしていきましょう。
まとめ
★加比の理(かひのり)★
比率A:Bと比率C:Dが同じである時、
(A+C):(B+D)の比や
(A-C):(B-D)の比はA:Bと同じになる

