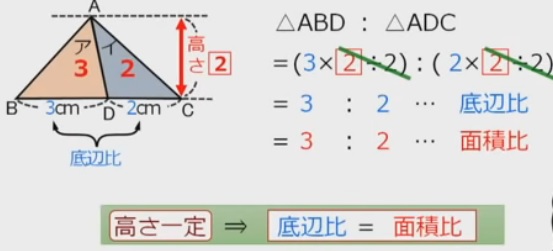
●高さが等しい三角形→底辺比=面積比●
●三角形が相似の場合、面積比は相似比の2乗と同じ●
この2点が基本となります。
面積比は高さの等しい三角形の組を探す!
画像出典:https://www.youtube.com/watch?v=o2cqvSa7jv0
高さが等しい三角形→底辺比=面積比
これは、基本の公式です。下記で書きますが、三角形が相似の
場合は面積比は相似比の2乗と同じになるので注意が必要です。
三角形の面積比のテクニック①:高さが同じ三角形を探し、それらの組み合わせに注目
三角形の面積比のテクニック①:高さが同じ三角形を探し、それらの組み合わせに注目
高さが等しい三角形→底辺比=面積比
なので、三角形に分けられた図形の面積比を考える場合、高さが同じ三角形を
探し、それらの組み合わせに注目するというテクニックがあります。

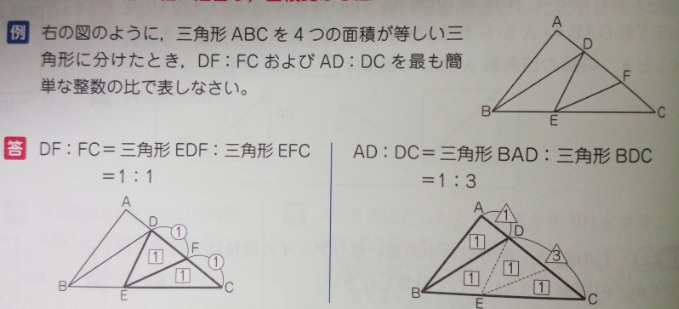
図の出典:『塾技100』p136
三角形の面積比のテクニック②:面積比が分かると底辺の比が分かる
三角形の面積比のテクニック②:面積比が分かると底辺の比が分かる
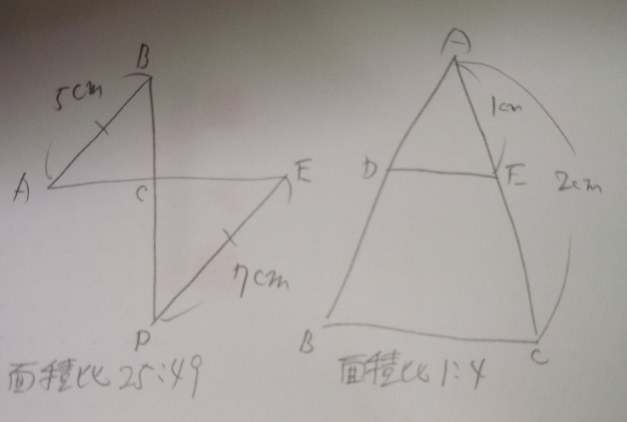
三角形の面積比は相似比の2乗と同じ
これは一種のパターンになっています。
●三角形が相似の場合、面積比は相似比の2乗と同じ●

「三角形が相似」の時です。
左の図の場合、辺ABとDEが平行でないと相似になりませんので注意してください。
三角形が相似であれば、面積比は相似比の2乗と同じ
になります。
左図:相似比5:7→面積比25:49
右図:相似比1:2→面積比1:4
三角形の面積比の中学受験問題等
問題)獨協埼玉中学
ACの長さが24cmである三角形ABCを、図のように面積の
等しい6つの三角形に分けます。この時、次の問いに答えましょう。
(1)AP:PCをもっとも簡単な整数の比で表しなさい
(2)PR:RCを最も簡単な整数の比で表しなさい
(3)RTの長さを求めなさい
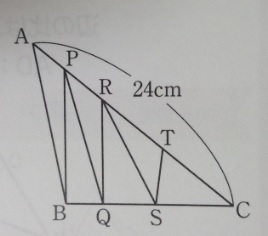
(1)6つの三角形の面積はすべて同じなので、面積比=底辺比。
△BAPと△BPCは高さが同じなので、AP:PC=面積比となる。
AP:PC=1:5(同じ面積の三角形が何個あるか数えれば良い)
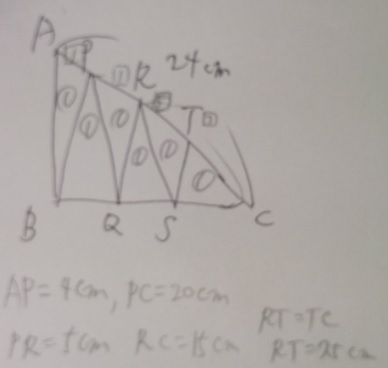
(2)(1)と同じ考え方で、PR:RC=1:3
(3)AP:PC=1:5 PR:RC=1:3なので
PC=20cm、RC=15cm、RT7.5cm

答え)(1)1:5(2)1:3(3)7.5cm
まとめ
●高さが等しい三角形→底辺比=面積比●
●三角形が相似の場合、面積比は相似比の2乗と同じ●
三角形の面積比のテクニック①:高さが同じ三角形を探し、それらの組み合わせに注目
三角形の面積比のテクニック②:面積比が分かると底辺の比が分かる