「三角定規」比率の基本と試験に出るポイントを抑えておきましょう。
90°/60°/30°の三角定規は最も短い辺と長い辺の比は1:2
90°/45°/45°の三角定規は長い辺を底辺とすると「高さ」と「底辺」の比は1:2
↓ ↓
【中学入試の算数受検問題上のポイント!】
1 「30°」「60°」「45°」という数字を見たら【比】の利用を考える
2 「30°」なくても【自分で作れないか】を考える(150°、135°、120°でピンと来る!)
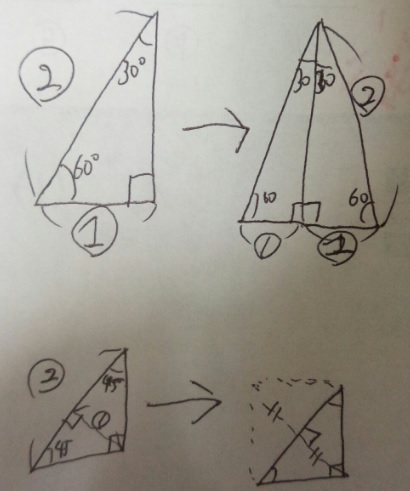
90°/60°/30°の三角定規は最も短い辺と長い辺の比は1:2
90°/45°/45°の三角定規は長い辺を底辺とすると「高さ」と「底辺」の比は1:2
図を見ると分かるかと思います。
試験的なポイントは、
1 「30°」「60°」「45°」という数字を見たら【比】の利用を考える
2 「30°」がなくても【自分で作れないか】を考える(150°、135°、120°でピンと来る!)
です。
基本問題は
「30°」「60°」「45°」という数字を見たら【比】の利用を考える
でいけますが、応用系は、
「30°」がなくても【自分で作れないか】を考える(150°、135°、120°でピンと来る!)
が大事になります。
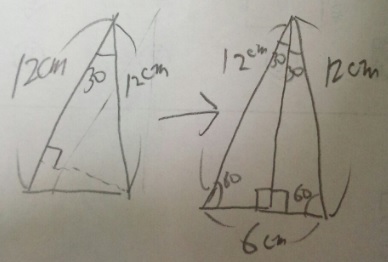
問題)1辺12cmの二等辺三角形で頂点の角度30°です。面積は?
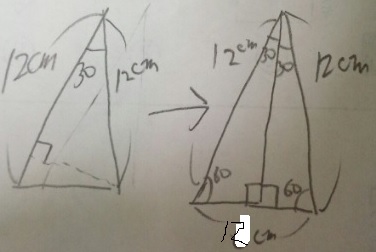
1)12cmの辺を底辺にした高さがわかれば良い
2)頂点が30°なので、直角(高さ)を作ると残りは60°
3)右図のように30°60°90°の三角形をくっつけると1辺12cmの正三角形
4)当初の二等辺三角形の高さは6cmとわかる(大丈夫ですか?)
5)12×6÷2=36 答え)36cm2
*このパターンが基本ですが、応用も基本の変化でしかありません!!
問題)この図の三角形の面積は?
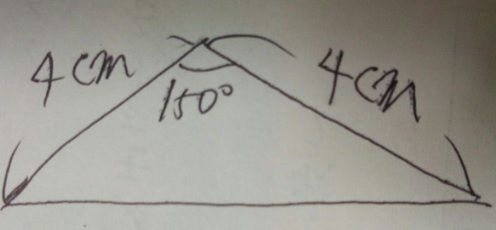
(必ず自分で図を書いて解いていく事!!)
1)まず、二等辺三角形ですね?150°以外の角度は15℃ずつ
2)150°を見たらピンとくる!「30°」を作れる
3)以下下の図を参照。
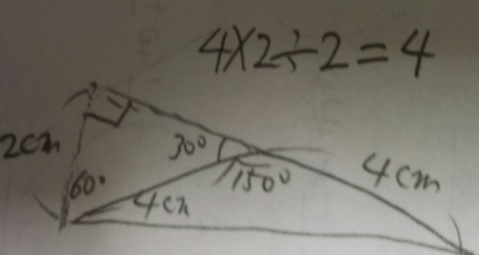
答え)4cm2
三角定規の辺の比(90/60/30と90/45/45)の中学入試問題等
問題)聖光学院中学
図1のように半径10cm、中心角90°のおうぎ形AOBがあり、おうぎ形の曲線AB
の部分を3等分した点をAから近い方からC、Dとします。図2のように点Aと
点Cを直線で結んでできる「ア」の部分の面積は何cm2ですか?円周率は3.14
*必ず自分で図を書いて書き込んでいってください
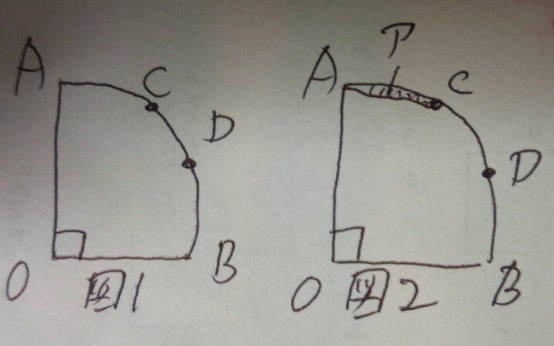
1)分かる所を図に書いていきます
2)おうぎ形AOC-三角形AOC=「ア」ですね?
3)AOもACも半径なので10cm、角度AOCは90度の三分の一なので30°
という事は、AからOCに直角の線を引くとそれは5cm(三角形AOCの高さ)
90°/60°/30°の三角定規は最も短い辺と長い辺の比は1:2
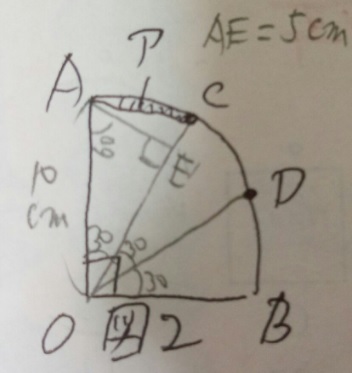
4)三角形AOCの面積は10×5÷2=25 25cm2
5)おうぎ形AOCの面積は、10×10×3.14×30/360
=314×1/12=314/12=157/6
6)157/6-25=26と1/6-25=1と1/6
157/6-25=157/6-150/6=1と1/6でも同じ
答え)1と1/6cm2
できましたか?分からなければ解法を何度も見て自分で解けるまでやってください。
まとめ
「三角定規」比率の基本と試験に出るポイントを抑えておきましょう。
90°/60°/30°の三角定規は最も短い辺と長い辺の比は1:2
90°/45°/45°の三角定規は長い辺を底辺とすると「高さ」と「底辺」の比は1:2
↓ ↓
【中学入試の算数受検問題上のポイント!】
1 「30°」「60°」「45°」という数字を見たら【比】の利用を考える
2 「30°」なくても【自分で作れないか】を考える(150°、135°、120°でピンと来る!)
