三角形の面積比の③つめです。
面積比=底辺比×高さ比のパターン
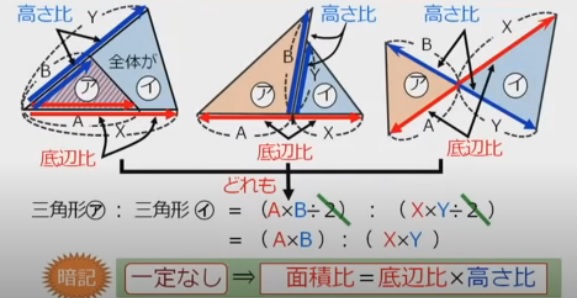
【面積比=底辺比×高さ比のパターン】について。
画像引用:https://www.youtube.com/watch?v=o2cqvSa7jv0
三角形の面積の比率についてはこれまで、
★加比の理(かひのり)★
比率A:Bと比率C:Dが同じである時、
(A+C):(B+D)の比や
(A-C):(B-D)の比はA:Bと同じになる
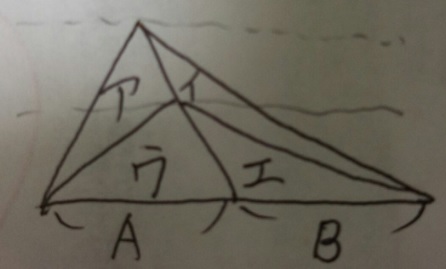
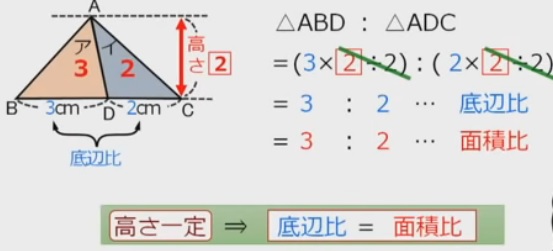
【ア(の面積):イ(の面積)=A:B】
(参考:加比の理(かひのり)と三角形の面積比②)
について学びました。
ここでは、
【面積比=底辺比×高さ比のパターン】について。

画像引用:https://www.youtube.com/watch?v=o2cqvSa7jv0
覚えてください。上記の図を見ればそれなりに分かるかと思います。
一番左端に関しては、以下のように覚える事も大事です。
【1組の角度が同じ三角形の面積比は、その角をはさむ2辺の長さ積の比と同じ】
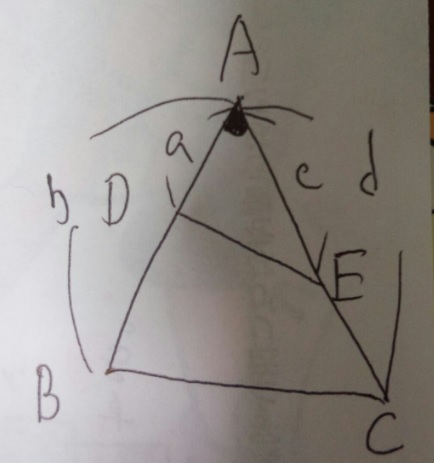
角度Aが等しいので、
三角形ADE:三角形ABC=(a×c):(b×d)
が成り立ちます。
問題)AD:DB2:3、AF:FC-=2:1、BE=ECの時、三角形DEFと三角形ABCの
面積比をもっとも簡単な整数比で表してください。
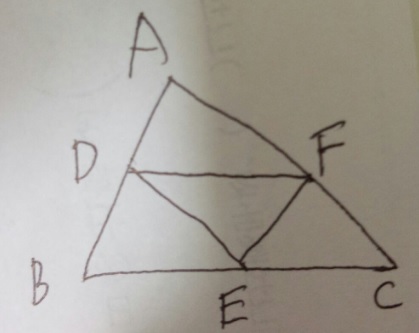
1)分かる事を図に書き込みます(必ず自分で図を書いてください!)
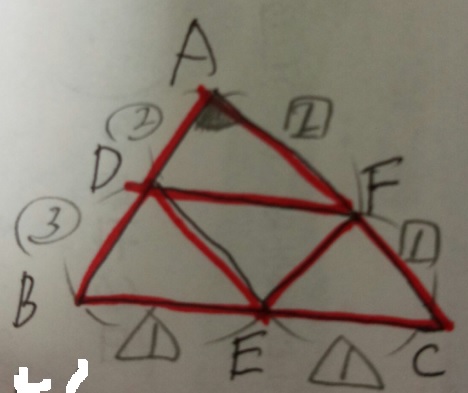
2)解法を考えましょう。う~~ん、う~~ん。
三角形DEFと三角形ABCの面積比!ひらめいた。
全体からDEFの周りをひけばいいんじゃね?
【1組の角度が同じ三角形の面積比は、その角をはさむ2辺の長さ積の比と同じ】
3)・三角形ADF:三角形ABC=(2×2):(5×3)=「4」:「15」
・三角形BDE:三角形BAC=(3×1):(5×2)=③:⑩
・三角形CEF:三角形CBA=(1×1):(2×3)=【1】:【6】
これで、DEFの周りの小さい三角形と三角形ABCのそれぞれの比率は出ました。
これを「連比」で揃えないといけませんね。連比は大丈夫ですよね?
「4」:「15」
⑩ :③
【6】 :【1】
三角形ABCの比率を最小公倍数の30で揃えます。
8:30
30:9
30 :5
これで比率は揃いました。

三角形ABCが30、三角形ADF8、三角形BDE9、三角形CEF5
求める三角形DEF=ABC-ADF-BDE-CEF
30-8-9-5=8
三角形DEFと三角形ABCの面積比は8:30
(もっとも簡単な整数比なので)4:15
答え)4:15
面積比=底辺比×高さ比のパターンの中学入試問題等
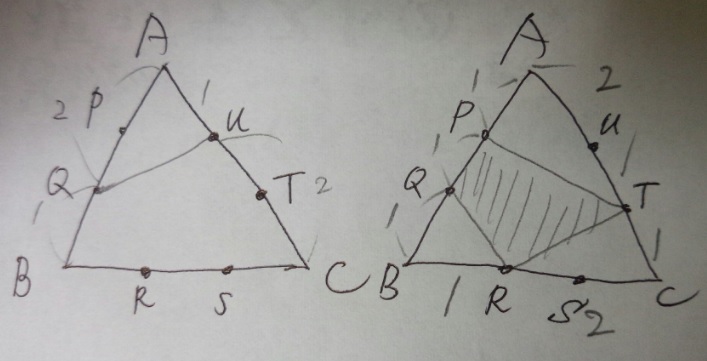
問題)巣鴨中学
正三角形ABCで辺上の各点はそれぞれの辺を3等分しています。
(1)三角形AQUの面積と正三角形ABCの面積の比を最も簡単は整数の比で答えてください
(2)四角形PQRTの面積と正三角形ABCの面積の比を最も簡単な整数の比で答えてください
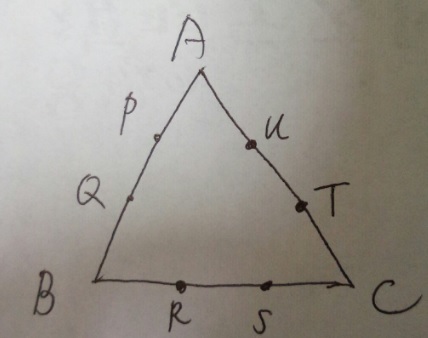
(1)三角形AQUの面積と正三角形ABCの面積の比
これはシンプルにできそうです。
【1組の角度が同じ三角形の面積比は、その角をはさむ2辺の長さ積の比と同じ】
三角形AQU:三角形ABC=(2×1):(3×3)=2:9

(2)四角形PQRTの面積と正三角形ABCの面積の比を最も簡単な整数の比で答えてください
【1組の角度が同じ三角形の面積比は、その角をはさむ2辺の長さ積の比と同じ】
これは【全体(ABC)-PQRTの周りの三角形】でできそうですね。
・三角形ABC:三角形APT=(3×3):(1×2)=9:2
・三角形BCA:三角形BRQ=(3×3):(1×1)=9:1
・三角形CBA:三角形CRT=(3×3):(2×1)=9:2
三角形ABCの比率はすべて9で揃っているのでそのままいけます。
四角形PQRTの面積比=三角形ABC-APTーBRQーCRT
=9-2-1-2=4 答え)4:9
答え)(1)2:9 (2)4:9

まとめ
【面積比=底辺比×高さ比のパターン】について。

画像引用:https://www.youtube.com/watch?v=o2cqvSa7jv0
一番左端に関しては、以下のように覚える事も大事です。
【1組の角度が同じ三角形の面積比は、その角をはさむ2辺の長さ積の比と同じ】

角度Aが等しいので、
三角形ADE:三角形ABC=(a×c):(b×d)
が成り立ちます。