
周期算とは?
「周期算」とは、文字通り、数字等が「周期的」に繰り返し並ぶ問題です。
「周期算」の基本的な問題は周期的な数字がいくつか示されて、
「n番目の数は?」「n番までの数の和は?」といった問題です。
周期算のポイント:「1グループ」と「あまり」
周期算のポイントは、
1)「周期=1グループ」を把握する事
2)「あまり」が大事:0ならグループ最後の数、1なら最初の数
「周期算」の基本的な問題は周期的な数字がいくつか示されて、
「n番目の数は?」「n番までの数の和は?」といった問題です。
問題)1,2,3,3、1,2,3,3、1,2,3,3という決まりにしたがって数字が
並んでいます。(1)15番目の数は?(2)15番までの数の和は?
解法)(1)15番目の数は?
1)「周期=1グループ」を把握する事
「1,2,3,3」 「1,2,3,3」 「1,2,3,3」
OK?
2)「あまり」が大事
1グループが数字4個(「1,2,3,3」)なので、
15÷4=3あまり3
「1,2,3,3」が3つあって、さらに3あまる
3あまるので、「1,2,3」ここが15番目の数。答え)3
「1,2,3,3」 「1,2,3,3」 「1,2,3,3」(1,2,3)
解法)(2)15番目までの数の和は?
1)これは1グループの和が必要です:1+2+3+3=9
2)15番目までなので、「1グループ」×3とあまり3ですね?
3)9×3+(1+2+3)=33 答え)33
答え)(1)答え)3(2)答え)33
周期算の一つ「循環小数」
小数点以下の数字が割り切れずに、同じ周期を繰り返すものを「循環小数」
と言います。循環小数を使った周期算の問題がよく出されます。
「循環小数」の問題の解き方も「周期算」と基本は同じ
1)「周期=1グループ」を把握する:実際に割っていく
2)「あまり」が大事:あまり0ならグループ最後の数、あまり1なら最初の数
問題)1/7を小数で表した時、小数第50位の数はいくつですか?
1)実際に割って「周期(グループ)」を見つけます。図を見てください。
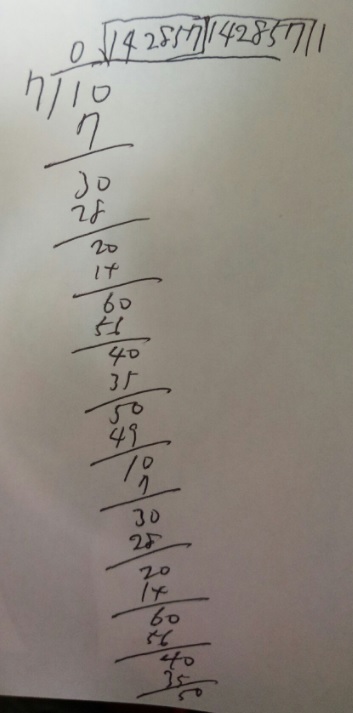
2)「1・4・2・8・5・7」が1グループですね?数字6個
3)小数第50位の数ですから、50÷6=8あまり2
4)「1・4・2・8・5・7」が8個あって、あまり2なので「1・4」
答え)4
「循環小数」の問題の解き方も「周期算」と基本は同じ
1)「周期=1グループ」を把握する:実際に割っていく
2)「あまり」が大事:あまり0ならグループ最後の数、あまり1なら最初の数
周期算:「1グループ」と「あまり」がポイントの中学入試問題等
問題)多摩大附属聖ヶ丘中学
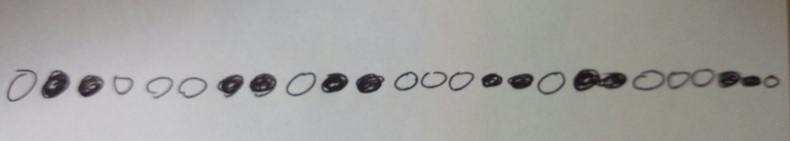
(1)左から50番目のご石の色は白ですか?黒ですか?
(2)左から229番目までに白いご石は何個ありますか?
(3)左から黒いご石だけを数えた時、127番目の黒いご石は白と黒を
合わせて左から何番目にあたりますか?
解法)(1)左から50番目のご石の色は白ですか?黒ですか?
1)何はともあれ、1グループを確認:「白、黒、黒、白、白、白、黒、黒」8個の石で1グループ
2)50÷8=6あまり2、「白、黒、黒、白、白、白、黒、黒」が6個+「白、黒」答え)黒

解法)(2)左から229番目までに白いご石は何個ありますか?
1)「1グループに8個」「1グループに白と黒が4つずつ」です
2)229番目:229÷8=28あまり5
3)28グループ+「白、黒、黒、白、白」です
4)28×4=112、それに白が3個なので112+3=115 答え)115個

解法)(3)左から黒いご石だけを数えた時、127番目の黒いご石は白と黒を
合わせて左から何番目にあたりますか?
1)「1グループに8個」「1グループに白と黒が4つずつ」です
2)「127番目の黒いご石」なので127÷4=31あまり3
3)31グループ+「白、黒、黒、白、白、白、黒」これですね?
4)31グループ+7個目が全体での何番目になります。31×8+7=255 答え)255番目
答え)(1)答え)黒(2)答え)115個(3)答え)255番目
問題)東邦大附属東邦中学
3を10回かけ合わせた数と、7を6回かけ合わせた数の積を求めると
一の位の数はどんな数になりますか?
1)(3×3×3×3×3×3×3×3×3×3)×(7×7×7×7×7×7)
だが、これをそのままやれということではない(入試では時間がなくなる)
2)すべて掛け算なので順番は変えられる、
(「3×7」×「3×7」×「3×7」×「3×7」×「3×7」×「3×7」)×3×3×3×3
3)一組「21」が6個、1の位が1なので何回かけても1の位は「1」
4)3×3×3×3=81
5)1の位が「1」の数字×81なので、一の位は「1」
答え)1
より周期算的に、「3、3×3=9、3×3×3=27、3×3×3×3=81、3×3×3×3×3=243」
なので、1の位は「3,9,7,1」の周期。なので、3を10回かけた1の位は、「1×3×3」=9
同じく、「7、7×7=49、7×7×7=1の位は3、7×7×7×7=1の位は1、次は7、次は9」
なので、7を6回かけた1の位は「9」と分かる。
9×9=81なので、答え)1
というやり方もありえます。
まとめ
周期算のポイントは、
1)「周期=1グループ」を把握する事
2)「あまり」が大事:0ならグループ最後の数、1なら最初の数
(関連記事)