必ず先に、下記の【旅人算の「基本」】を読んでください。
ここでは、「池のまわりを回る系」問題を押さえた上で、「旅人算」の
実際の中学入試問題を難問か解きながら、マスターしていってもらおうと思います。
【旅人算の「基本」】をおさらい
●二人の進行方向が同じ場合(追いつき算)
→追いつく時間=2人の間の距離÷2人の速さの差
●二人の進行方向が反対の場合(出会い算)
→出会う時間=2人の間の距離÷2人の速さの和
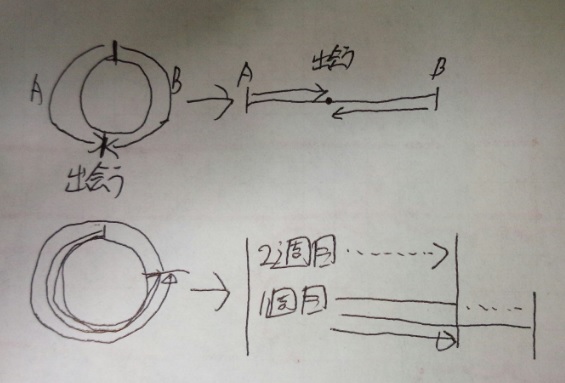
旅人算の「池のまわりを回る系」問題も「直線」で考えられる
旅人算には「池のまわりを回る系」問題があります。
(慣れればどちらでもいいのですが)円で考えても、直線で考えてもどちらでも
解けます。直線の方がやりやすければ直線でやってください。
「池のまわりを回る系」問題の考え方
1)逆向きに進む:出会い算
1-1 2人の進んだ距離の和=池1周の長さ
1-2 2人の速さの和×出会うのにかかる時間=池一周の長さ
2)同じ向きに進む:追いつき算
2-1 (速い方は2週目になるので)2人の進んだ距離の差=池一周の長さ
2-2 2人の速さの差×追いつくのにかかる時間=池1周の長さ
*速い方が遅い方より池一週分多く周っているということやね

上が【追いつき】系、下が【出会う系】
問題)池の周りを、A,B,Cが同時に同じ地点を出発して周ります。Aは
分速60m、Bは分速□mで同じ向きに、Cは分速40mで逆向きに進み始め
ました。CとBは10分後に出会い。さらにその7分後にAと出会いました。□は?
解法)
1)AとCが出会うのは、10+7=17分後
2)AとCは出会い算なので、17分×100m/分(2人の速さの和)=1700m(池の長さ)
3)CとBは10分後に出会っているので、1700=(40+□)×10、40+□=170、□=130
答え)130
問題)池の周りをA、Bが同じ場所から同じ方向にまわります。Aは分速90m、
Bは分速60m。Aは12分後にBを追い越しました。池の回りは何m?
解法)
1)速さの違う2人が同じ方向にいくので追いつき算です:2週目に追いつく
2)2人の速さの差は90-60=30m/分
3)速い方が2週目になるので、2人の進んだ距離の差=池一周
4)Aは1080m進む、Bは720m進む。1080-720=360m
(2人の速さの差×追いつくのにかかる時間=池1周の長さ
を使っても良いですが、なぜそうなるのかをしっかり理解してください。)
答え)360m
旅人算(応用)の中学入試問題等
問題)青山学院中等部
あき子さんと兄が家から同じ道をポストに向かってそれぞれが一定の速さで
歩いています。8時にあき子さんはポストまで357mの地点にいて、兄の63m
前方にいました。兄は8時3分にあき子さんを追い越し、8時5分にポストに
着いて、すぐに同じ道を引き返しました。兄があき子さんと出会うのはポスト
から□mの地点です。
解法)
1)線分図的な図を書きましょう。方向同じなので【追いつき算】ですね
2)先に出ていたのがあき子さんで、兄の方が速いようです
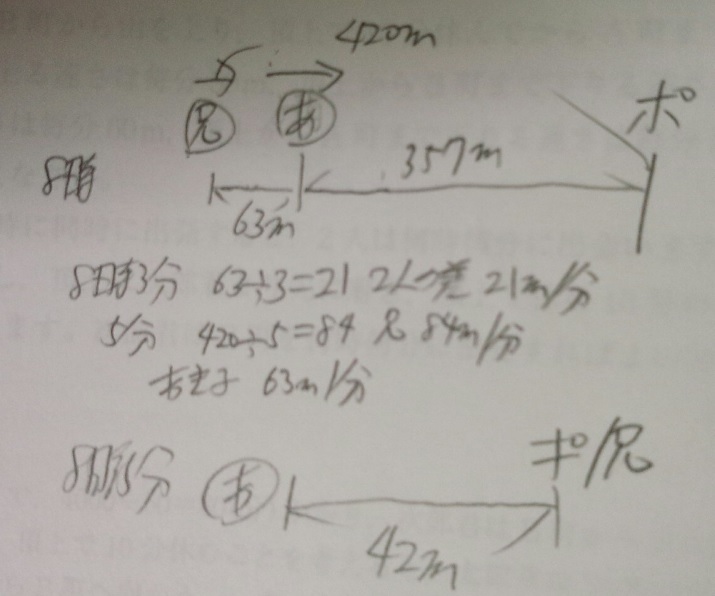
3)8時に63mの差があったのが3分で追いついていますので、2人の速さの差は21m/分
4)8時の時点で兄とポストの差は(357+63)=420mなので兄の速さは420÷5=84m/分
あき子さんの速さは、84-21=63、63m/分
5)8時5分の時点であき子さんとポストの差は357-(63×5)=42m
6)42mの出会い算で、二人の速さの和は147m/分、42/147=2/7
7)8時5分から2/7分後に二人は出会う、ポストと兄が同じ位置なので、
兄が2/7分で進んだ距離が二人が出会った時のポストからの距離。2/7×84=24 24m
答え)24 (問題が数字だけを聞く形になっているので答えは数字だけ)
まとめ
●二人の進行方向が同じ場合(追いつき算)
→追いつく時間=2人の間の距離÷2人の速さの差
●二人の進行方向が反対の場合(出会い算)
→出会う時間=2人の間の距離÷2人の速さの和
「池のまわりを回る系」問題の考え方
1)逆向きに進む:出会い算
1-1 2人の進んだ距離の和=池1周の長さ
1-2 2人の速さの和×出会うのにかかる時間=池一周の長さ
2)同じ向きに進む:追いつき算
2-1 (速い方は2週目になるので)2人の進んだ距離の差=池一周の長さ
2-2 2人の速さの差×追いつくのにかかる時間=池1周の長さ
*速い方が遅い方より池一週分多く周っているということやね

必ず先に、下記の【旅人算の「基本」】を読んでください。