分数の計算自体はそれほど難しくはないですが、色々な問題を解く際に
分数を使いますので、必ずマスターしましょう。
全ての勉強に共通していますが、
「正しいやり方を覚える+問題をたくさん解く(量をこなす)」
がマスターする基本です。
分数のたし算
1 通分する(分母を揃える)
2 分子同士を足し算する
3 (必要であれば)約分する
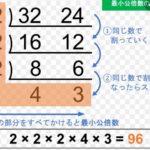
「通分」をするためには、「最小公倍数」が分かっていないと
できませんので、まだの方はそちらが先です。「最小公倍数」に
ついては下記記事をどうぞ。
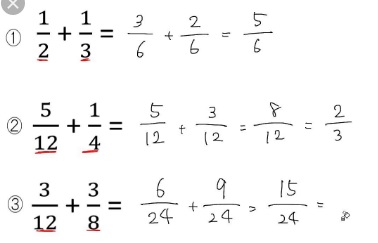
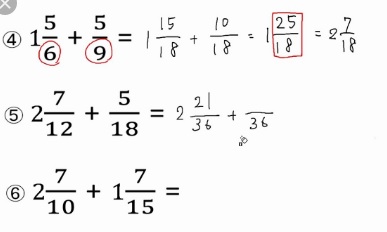
1 通分する(分母を揃える)
「通分」は最小公倍数にするために分母にかけた数字を、分子にもかけます。
1/2=2/4=3/6=4/8
×2/2 ×3/3 ×4/4
2 分子同士を足し算する
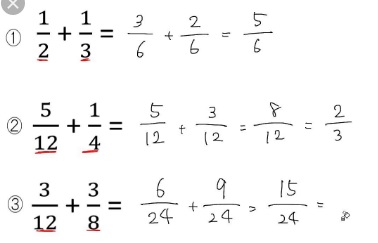
分母は変えずに、分子のみを足します。
基本的にこれで、分数のたし算は答えが出ます。
3 (必要であれば)約分する
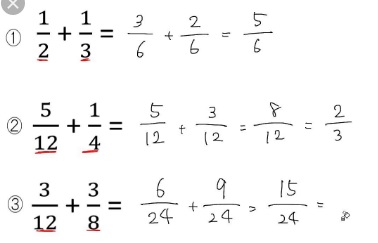
分母、分子ともに、まだ割れる数(公約数)があれば、約分します。
分数のひき算
1 通分する(分母を揃える)
2 分子同士をひき算する
3 (必要であれば)約分する
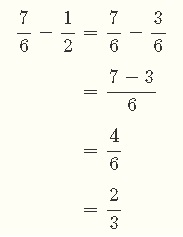
分数の引き算は、基本的に分数のたし算と同じやり方です。
分数のかけ算
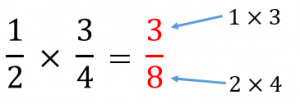
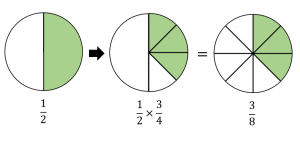
1 分子同士・分母同士をかける(通分する必要はありません)
2 分母と分子で約分できる時は先に約分する(分母同士、分子同士は約分しません)
帯分数のかけ算は、一度仮分数に直してからやります。
分子同士、分母同士をかけるのは同じです。
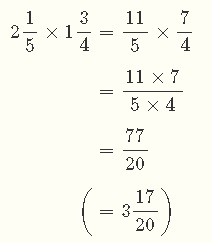
問題)
2/5×2/3
3/10×1/6
分数の割り算
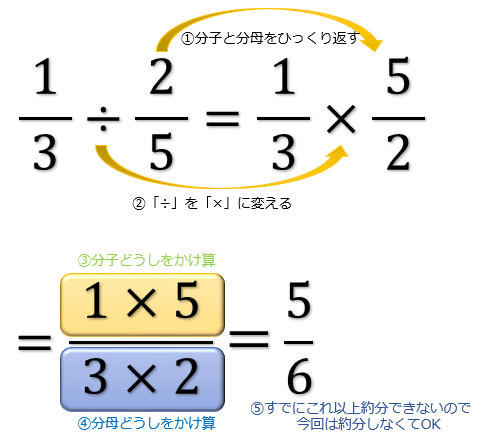
分数の割り算は、割る数の分母と分子をひっくり返して(逆数)
からかけ算をします。そこからは分数のかけざんと同じです。
分母と分子で約分できるものがある場合にはします。
整数の場合は分母を「1」にして考えます(分母1の分数に直す)。
3/8÷4=3/8÷4/1=3/8×1/4=3/32
帯分数の割り算は、一度仮分数に直してからやります。
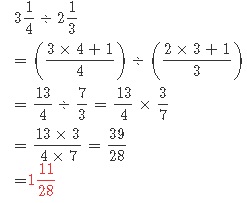
問題)
8/15÷3/5
2/7÷3/5
9/7÷3/5
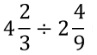
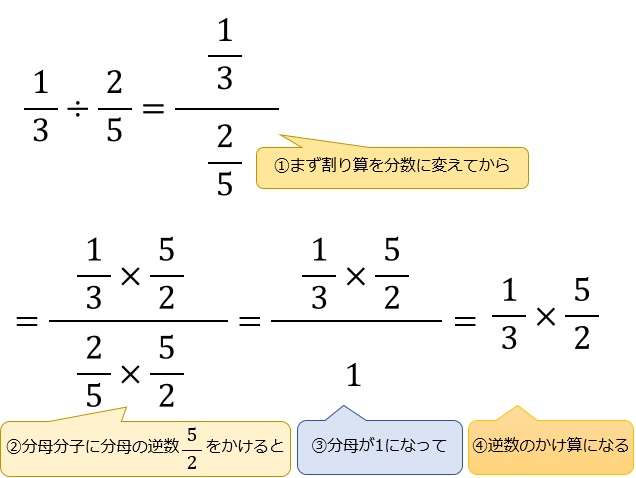
「分数の割り算の考え方」
2÷5=2/5というように、割り算は分数に変形できます。
(4÷2=4/2=2、9÷3=9/3=3)
この考え方を分数の割り算に応用すると、「分数の分数」になります。
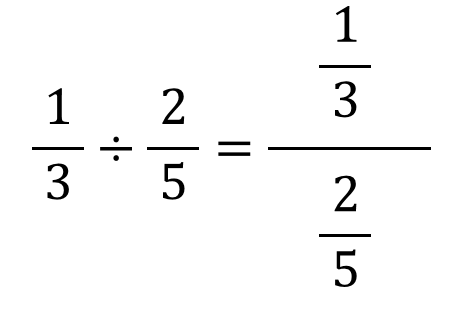
この式をシンプルにするために、分母を「1」にしましょう(約分や通分
と同じ考え方)。