三角形の面積を求める問題は中学入試によく出ますが、
残念ながら単に公式に当てはめる問題はほぼありません。
必要となるテクニックは、例えば、
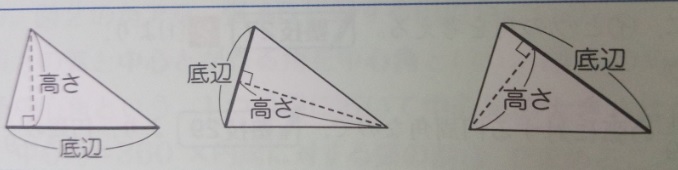
●同じ図形でも「底辺」「高さ」を変えて2通りの方法で面積を表す
●補助線を引く(直角等を作る)
といった事が必要になります。
とはいえ、基本の公式を知らないとまずは話になりませんので、
まずは基本をおさえましょう。基本を徹底した上ではじめて
応用ができるようになります。
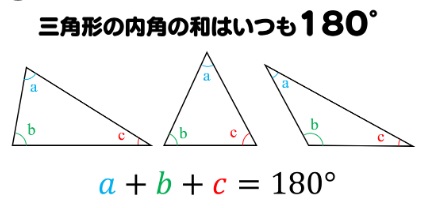
三角形の角度
三角形の内角の和は180度。3つの角度を足すと必ず180°になる。
直角二等辺三角形

直角(90度)以外の二つの角度は45度。
正三角形と直角三角形
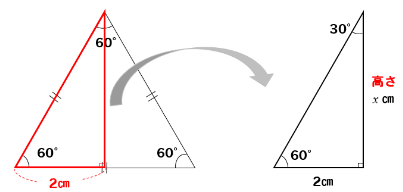
正三角形はすべての角度が60°。
正三角形を半分にすると「30°、60°、90°の直角三角形」になり、
一番長い辺が一番短い辺の2倍の長さになる。

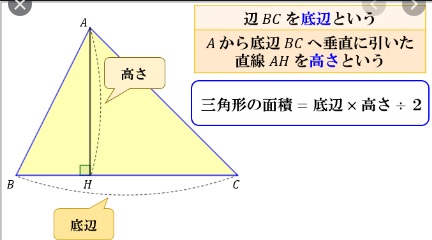
三角形の面積の公式―底辺×高さ÷2
三角形の面積の公式は
「底辺×高さ÷2」
です。
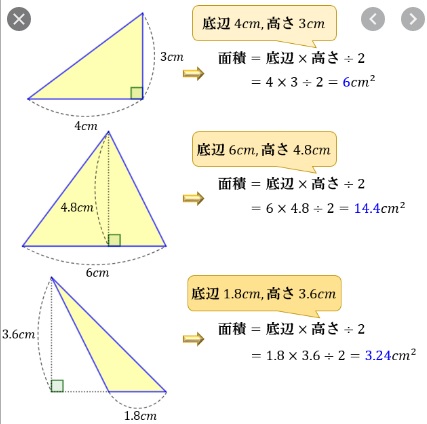
三角形の面積の求め方の3つのテクニック!
三角形の面積を求める問題は中学入試によく出ますが、
残念ながら単に公式に当てはめる問題はほぼありません。
必要となるテクニックは、例えば、
1 同じ図形でも「底辺」「高さ」を変えて2通りの方法で面積を表す
2 補助線を引く(直角等を作る+分けて考える)
3全体から不要な部分を引く事で求める
といった事が必要になります。
1 同じ図形でも「底辺」「高さ」を変えて2通りの方法で面積を表す

同じ三角形でも、どの辺を「底辺」にするかで「高さ」は
変わります。ですので「補助線を引く」とセットで考えて、
2通りの方法で面積を表せるようにしましょう(面積2通りの法)。
「補助線」を引くのは、図形の問題では絶対に
必要な事ですので、必ず「どういう補助線を引けばいいのか」を
考える習慣をつけておきましょう。
三角形であれば、「直角を作るために補助線を引く」事が多い
ですが、「平行線ならば錯角」を作るためにという事になります。
例題)下記の直角二等辺三角形の面積をそれぞれ求めましょう
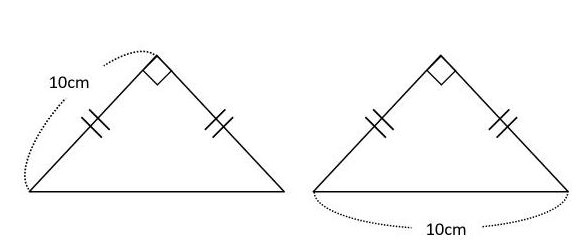
解法)
左側は底辺10cm、高さ10cmという事がすぐに分かりますね?
三角形の面積の求め方は「底辺×高さ÷2」ですから、
10×10÷2=50
答え)50cm2
右側の直角二等辺三角形はどうでしょう?
考えてみましょう。
分かりましたか?
補助線を引く(直角等を作る)のテクニックを使います。
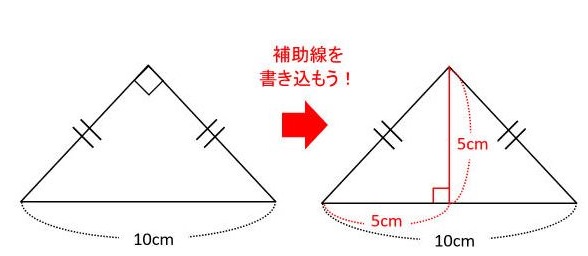
このように補助線を引くと、直角二等辺三角形が別の二つの直角二等辺
三角形になっている事が分かります。
10×5÷2=25
答え25cm2
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
正三角形はすべての角度が60°。
正三角形を半分にすると「30°、60°、90°の直角三角形」になり、
一番長い辺が一番短い辺の2倍の長さになる。

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
色々な三角形の問題の基本となる公式・考え方ですので、きっちりと
身につけましょう。
例題)下記の三角形ABCはAB=ACの二等辺三角形です。面積は?
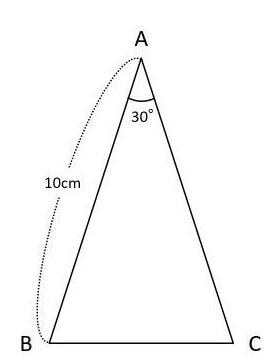
補助線を引く(直角等を作る)のテクニックを使います。
「30°」と見た時点で、
「「60°、90°」の正三角形を半分にした直角三角形だな、
短い辺が長い辺の半分のヤツだな」
とピンとくる必要があります。
AB=ACなのでどちらかを「底辺」にして「高さ」を作る
補助線を引きます。

正三角形はすべての角度が60°。
正三角形を半分にすると「30°、60°、90°の直角三角形」になり、
一番長い辺が一番短い辺の2倍の長さになる。
でしたね?ですので、BHは5cmと分かります。
10×5÷2=25cm2
答え)25cm2
2 補助線を引く(分けて考える)
以下のようなパターンは難易度が高い「補助線問題」です。
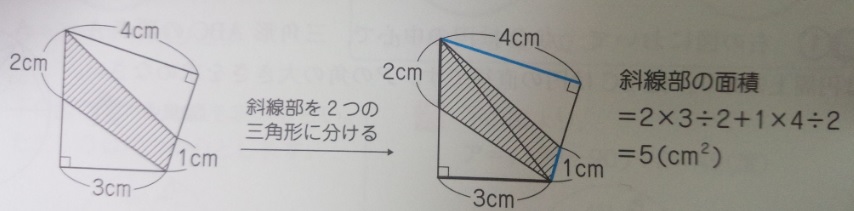
この
「補助線(対角線)を引いて二つの三角形を作り、直角を利用して面積を出す」
というのは、一つのパターンになっていますので、覚えてしまった方がいい
でしょう。
解法パターンの手続きとしては、
1「補助線(対角線)を引く」
2「三角形を2つ作る」
3「直角を利用して高さを設定し計算する」
です。
3 全体から不要な部分を引く事で求める
全体から不要な部分を引く事で求める
これも三角形の面積を求める際には有効な方法です。
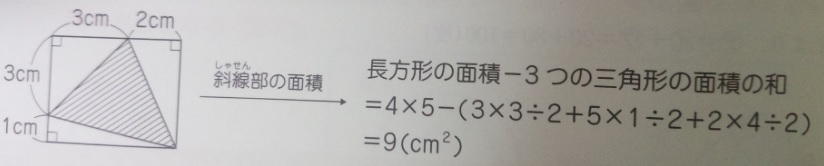
上記の形はシンプルな計算でできますが、中学受験問題、特に難関校
になってくると、上記のような形の図形に、正確な補助線を引かないと
解けない問題が出てきます・・・。
まずは基本からでいいかと。
まとめ
三角形の面積問題を解くテクニックは以下です。
1 同じ図形でも「底辺」「高さ」を変えて2通りの方法で面積を表す
2 補助線を引く(直角等を作る+分けて考える)
3全体から不要な部分を引く事で求める
上記を頭に入れて、たくさん問題を解いていきましょう。