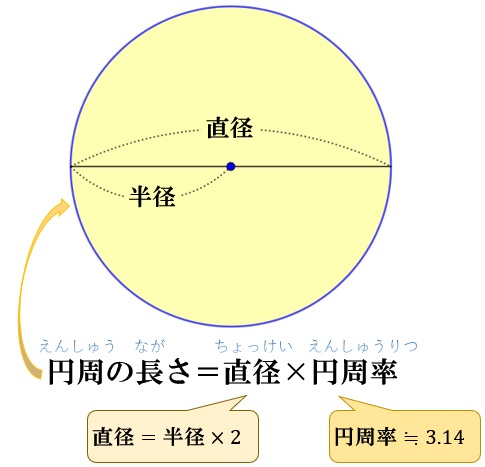
円周率の基本
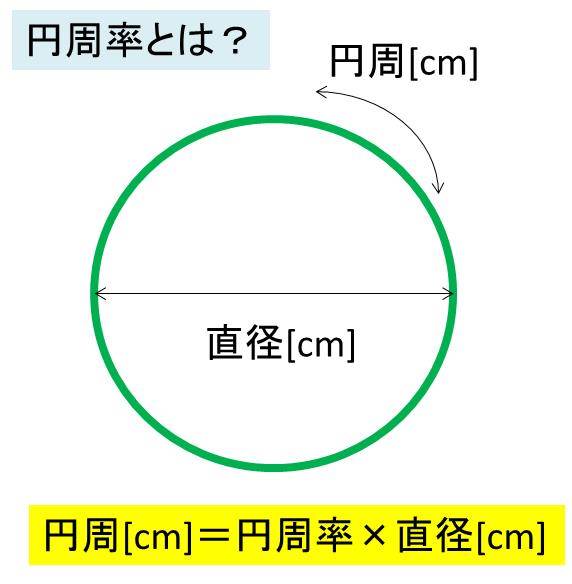
●円周の長さ=直径×円周率(3.14)
●円周率(3.14)=円周÷直径
円周率=円周÷直径は3.141592…と永遠に続く事が知られています。
円の周り(円周)の長さは、直径の3.14…倍という事です。
全ての円で、円周率は3.14…で同じです。
まずは円周率は3.14と覚えましょう。

画像出典:https://atarimae.biz/archives/25615
これは「基本」です。
残念ながら、中学受験では「基本」はできて当たり前で、できないと
そこで差をつけられます。逆に差をつけるには、基本を踏まえた上での
応用になります。
ここでは、「円周率の倍数」を暗記してしまいましょう。
分配算などでたくさん使われるものです。
円周率(3.14)の倍数は暗記する!
3.14はいわば有名な数字なので、誰でも知っています。
でも、それが半分になったり、3倍、5倍となるとどうでしょう?
■円周率の倍数(黄色数字を見たらピンと来ること)■
3.14×1/10(0.1)=0.314
3.14×1/5(0.2)=0.628
3.14×1/4(0.25)=0.785
3.14×1/2(0.5)=1.57
3.14×2=6.28
3.14×3=9.42
3.14×4=12.56
3.14×5=15.7
3.14×6=18.84
3.14×7=21.98
3.14×8=25.12
3.14×25(5×5)=78.5
3.14×36(6×6)=113.04
これらの数字は「円」の問題というよりは、計算の問題でよく
出てきます。いわゆる「分配算・分配法則」を使うものなどです。
計算問題などで「3.14」が出てきたら、周囲に、その倍数等が
ないかを注意するだけで全然違います。
0.785
1.57
6.28
12.56
等は頻出です。
例題)1.57×28-3.14×4 (東海大付属浦安高中等部)
3倍+0.14倍!
円周率の倍数は暗記するといっても、何も考えずに丸暗記しろとはいいません。
逆にそれは効率が悪いです。
「3.14」という事は、「3倍と少し」です。
下記の数字はすべて「3倍と少し」ですよね?
3倍はすべて暗記しているはずですので、0.14の方を計算するなり、繰り返し
くっつけるなりの練習をしていると自然と覚えていけるかと思われます。
3.14×2=6.28 3×2=6
3.14×3=9.42 3×3=9
3.14×4=12.56
3.14×5=15.7
3.14×6=18.84
3.14×7=21.98
3.14×8=25.12
3.14×25(5×5)=78.5
3.14×36(6×6)=113.04
「3.14」という事は、「3倍と少し」ですので、トンチンカンな
数字にだけはならないようにしましょう。
まとめ
■円周率の倍数(黄色数字を見たらピンと来ること)■
3.14×1/10(0.1)=0.314
3.14×1/5(0.2)=0.628
3.14×1/4(0.25)=0.785
3.14×1/2(0.5)=1.57
3.14×2=6.28
3.14×3=9.42
3.14×4=12.56
3.14×5=15.7
3.14×6=18.84
3.14×7=21.98
3.14×8=25.12
3.14×25(5×5)=78.5
3.14×36(6×6)=113.04
