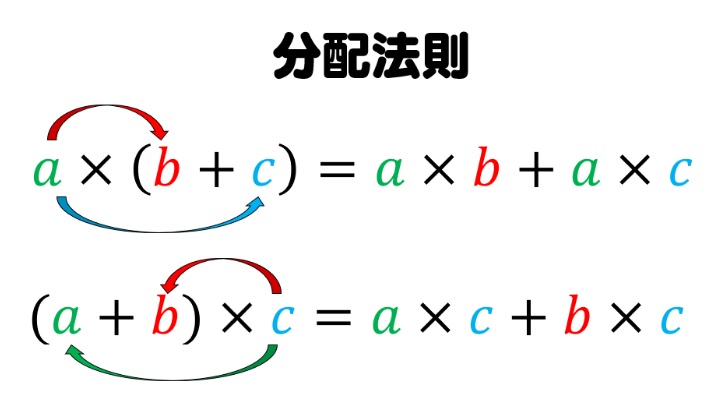
分配法則(計算の工夫)/a×b+a×c=a×(b+c)のyoutube音声動画
この記事のyoutube音声動画です。
音声を聞きながら記事を読んでいくとより分かり
やすいかと思います。
いきなり「分配法則」と言われても分からないと思いますが、
「算数の計算をする際の工夫」
と考えれば大丈夫です(そもそも名前に意味はありません)。
「交換法則・結合法則」の基本がまだの方は先にこちらの
記事をどうぞ。
ポイントは
【たし算と掛け算は順番を入れ替えても答えが変わりません】
です。
例題)8.42×24+1.58×24-5×24
こんな問題を前から正直やってたら時間が足りません。同じ数字(ここでは24)
を見たらピンと来ましょう。
8.42×24+1.58×24-5×24
=(8.42+1.58-5)×24
=5×24
=120
ポイントとしては
「「24」という同じ数に三つの数をかけているので、
それを「分配」して計算をしやすくする事ができる」
というテクニックがあるという事を覚えましょう。
こういった種類の計算問題は中学入試では頻出です。
●計算問題で1つの式に同じ数がいくつかあったら分配法則を使う可能性が高いです●
分配法則(算数の計算の工夫)で最も使うテクニック
a×b+a×c=a×(b+c)
8×10+8×2=8×(10+2)=96
a×b+a×c=a×(b+c)
このタイプの分配法則はかなりたくさん出てきますので、同じ数字がいくつか
出てくる計算問題があったら、「これは分配法則を使えって事かな?」と
ひらめく(受験的ではありますが・・・)センスが大事です。
極端に言うと、「分配法則」系の中学入試問題は、ほぼ全て、上記の基本
法則の応用(バリエーション)と考える事もできます。
図で見てみると分かりやすいかもしれません。
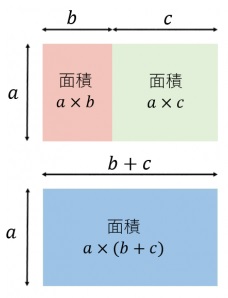
また、上の例は逆に考えると、二桁と一桁のかけ算は無意識に分配法則を
使っているという事でもあります。
12×8=(10+2)×8=8×10+8×2=96
この式を右から逆に辿れば分配法則の計算になります。
a×b+a×c=a×(b+c)
です!
算数(数学)ですから、(人生と違って・・・)公式にどんな数字を
入れても答えは必ず出ます。
a×b+a×c=a×(b+c)
2×12+2×9=2×(12+9)=2×21=42
例題)67×18+12×67
答え)67×(18+12)=67×30=2010
こういった問題を分配法則を使わずに、正面から正直に
解いてはいけないのでしょうか?
中学受験としてはダメでしょうね。時間がかかりすぎますし、
そもそも、問題を出す側は「分配法則を使えますか?」という
事を聞いていますので・・・。
それに、とても便利なので「分配法則」を覚えて使えるように
しましょう。
分配法則の割り算は(a+b)÷c=a÷c+b÷cは成立する
分配法則の割り算は(a+b)÷c=a÷c+b÷cは成立しますが、
a÷(b+c)=a÷b+a÷cは成立しません。
例題)525÷6-225÷6 (お茶の水女子大付属中)
答え)(525-225)÷6=50
これ位の問題であれば、「あれ、これは分配法則を使って良い割り算だっけ?」
と思ったら、頭から計算してもそんなに時間は変わらないかもしれません。
525÷6=87.5、225÷6=37.5 87.5-37.5=50
分配法則のテクニックを使う4つの場面
中学受験の算数で
a×b+a×c=a×(b+c)
の公式とその応用を使う場面は主に4つあります。
1 2桁以上の掛け算
2 2桁×2桁の掛け算の問題
3 円周率(3.14)を含む計算
4 図形の面積の計算
1 2桁以上の掛け算
これは上の方で説明したものです。再度書くと、以下のようになります。
8×10+8×2=8×(10+2)=96
a×b+a×c=a×(b+c)
算数は、「解き方(公式・テクニック)を覚えたら、数をこなす」のが
もっとも身につきますので、分配法則を使ってたくさん問題を解きましょう。
例題)20×33+20×17
例題)100×151-100×61-100×40
例題)4×3+4×5
答え)4×(3+5)=4×8=32
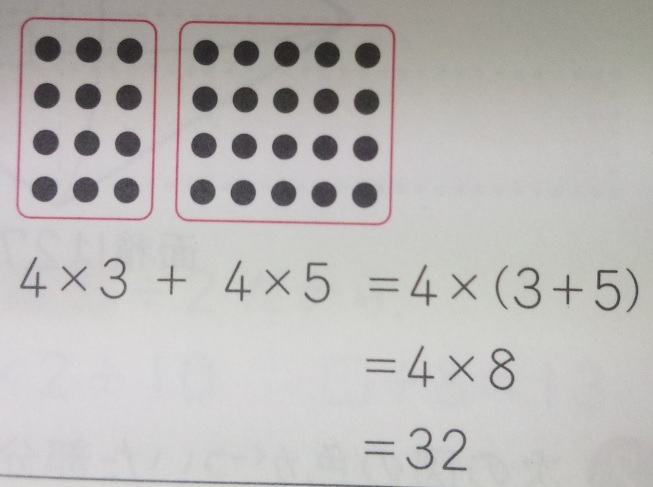
図で考えると分かりやすいかもしれません。
以下は【応用】になります。
中学受験の算数の問題でしばしば出てくるのは、
「分配算(分配法則)を使うために数を揃える」
というパターンです。入試問題の場合はほとんどがこの形です。
この場合、「交換法則・結合法則」も合わせて使います。
つまり、
1 たし算は順番を変えても答えは変わらない
2 掛け算は順番を変えても答えは変わらない
3 「100=4×25」のように工夫すると計算しやすい
ですね。
例題)670×1.8+12×67 (筑波大附属中)
素直にやると時間が足りませんし、間違えやすくなります。
670×1.8+12×67
=67×10×1.8+12×67
=67×18+12×67
=67×(18+12)
=67×30
=2010
答え 2010
ポイントは分配法則を使うために「67」にまとめている〔数をそろえる)事です。
例題)6.28×1.4-2.4×3.14+6.28×0.3
ポイント・テクニックは【分配算を使うために数を揃える】事です。
上記の問題では、「4×3.14」を「2×6.28」に変えてももちろん
答えは同じになります。
ですので、計算問題で分配法則を使うべきかどうかは、
「1 同じ数が式の中に複数ある時」(基本)
「2 割ったり、かけたりして同じ数にして分配法則を使う時」(応用)
この二つの視点で見ると良いかと思われます。
2 2桁×2桁の掛け算の問題
a×(b+c)=a×b+a×c
の場合、下記のパターンの問題がよくあります。
例題)101×99
もちろん、素直に解いても良いですが、時間がかかります・・・。
分配法則を使えという事ですね。
101×99=(100+1)×99=100×99+1×99=9999
例題)11×301
また、「結合法則」「交換法則」「分配法則」すべてを使った
掛け算なども良く出題されます。
大事なのは【頭を柔らかくする】ということでしょうか?
例題)12×11+7×22+2×33-8×44 (日大第一中)
この種の数字が出たら「ピン」とくる事が大事です。
「25 50 100 1000」とか「11 22 44 121」とかですね。
上記の問題では、
「分配算を使うために数を揃える」(22=11×2等)
という事をしていますが、この考え方は多くの問題で使います。
3 円周率(3.14)を含む計算
分配法則が非常に役に立つのは「円周率」関係の問題の時です。
ある種の「パターン」(テクニック)になっていますので、覚えて
しまうのが良いかと思います。
例題)色のついた部分の面積を求めなさい(円周率は3.14とする)
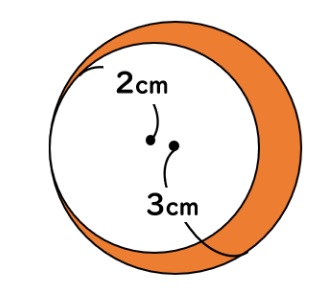
この問題を素直に解くと、半径3cmの円の面積から半径2cmの円の面積を
引くことで、色のついた部分の面積が出ますよね?
ですので、式としては、
【3×3×3.14-2×2×3.14】
となります。
これを素直に解いていくと、時間がかかります。中学受験の算数は最終的には
時間との戦いです。そして、(いやらしい事に)素直に解いていくと、時間が
足りなくなるようになっているのです・・・。世知辛い世の中ですね。
という事で分配法則を使って速く解く事が求められます。
同じ3.14で複数の数字をかけているので、
【(3×3-2×2)×3.14】
となります。ですので、
5×3.14=15.7
となり、答えは
15.7cm
になります。
また、円周率の3.14は普通の計算問題でもよく出てくるので、
【3.14=1.57×2=1.04×3=0.785×4=0.628×5】
【3.14×2=6.28 3.14×3=9.42 3.14×4=12.56】
これは暗記した方が良いです。
次の例題は難しいですが、何度か途中の式を見て、仕組みを
理解すればできるかと思います。
例題)3.14×5-0.785×12+1.57×8
(分配算を使うために「3.14」に合わせるのがポイントです)
4 図形の面積の計算
図形の面積の計算については図を見るのが一番です。
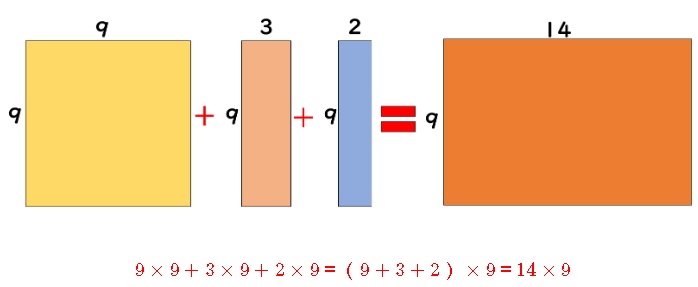
これはかなり簡単な図形ですが、基本の考え方は同じです。
図形については、図形のところで細かく見ていきたいと思います。
まとめ―分配法則(計算の工夫)/a×b+a×c=a×(b+c)
a×b+a×c=a×(b+c)
8×10+8×2=8×(10+2)=96
この公式が基本です。
ただ、公式そのままで入試問題が出題される事は少ないです。
そのために、
「分配算を使うために数を揃える」
という意識を持つ事が大事になります。
670×1.8+12×67 (筑波大附属中)
こういった問題ですね。
後は、多くの問題を解いて「分配法則」に慣れましょう。
上記問題集で練習してみましょう。
分配法則(計算の工夫)/a×b+a×c=a×(b+c)のyoutube音声動画
この記事のyoutube音声動画です。
音声を聞きながら記事を読んでいくとより分かり
やすいかと思います。


