円と正方形のルール2つ
1【円の中の正方形の面積は、その円の半径を1辺とする正方形の面積の2倍】
(円の半径×半径×2=正方形の面積)
2【半径×半径=円に内接する正方形の面積の半分】
(正方形の面積が与えられていれば円の半径(×半径)はすぐにわかる)

円の基本のおさらい
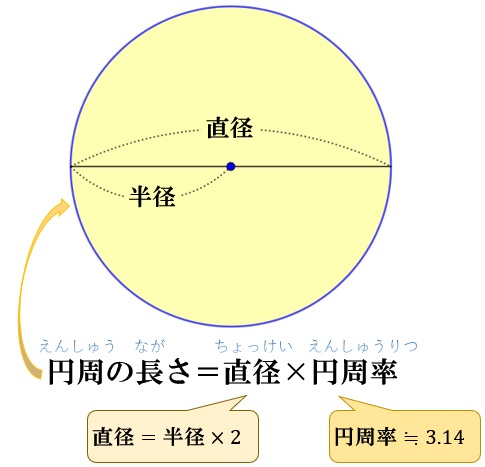

●円周の長さ=直径×円周率(3.14)
●円周率(3.14)=円周÷直径
●円の面積=半径×半径×円周率(3.14)
円周率(3.14)周辺の数字は暗記で
円周率(円周÷直径)の3.14は計算問題などにも多数出てきますね。
■円周率の倍数(黄色数字を見たらピンと来ること)■
3.14×1/10(0.1)=0.314
3.14×1/5(0.2)=0.628
3.14×1/4(0.25)=0.785
3.14×1/2(0.5)=1.57
3.14×2=6.28
3.14×3=9.42
3.14×4=12.56
3.14×5=15.7
3.14×6=18.84
3.14×7=21.98
3.14×8=25.12
3.14×25(5×5)=78.5
3.14×36(6×6)=113.04
この記事では「円と正方形」についてまとめています。
いわゆる「図形」の問題になります。
円と正方形

ルール1!
【円の中の正方形の面積は、その円の半径を1辺とする正方形の面積の2倍】
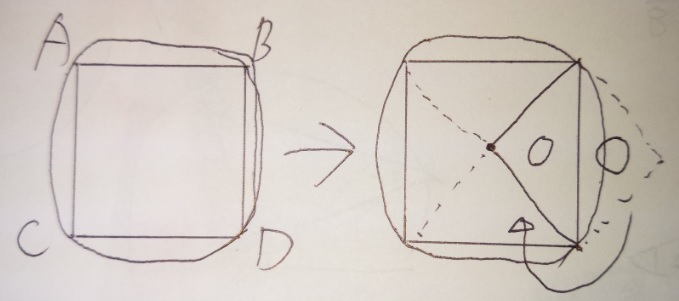
「円に内接する正方形」の図は算数の問題でよく出てきますが、
上記のルールをきちんと覚えて使いこなしましょう。
理由は図の通りです。四角形は三角形二つからできてますし、正方形の場合は図のようになります。
ですから、「円に内接する正方形」の場合、円の半径、もしくは
直径が分かれば、正方形の面積は求められます。

上記の図で仮に円の半径が3cmであれば、正方形の面積は、
3×3×2=18 18cm2 となります。
ルール2
【半径×半径=円に内接する正方形の面積の半分】

ルール1【円の中の正方形の面積は、その円の半径を1辺とする正方形の面積の2倍】を
少し変えるとルール2になります。
【半径×半径=円に内接する正方形の面積の半分】
ルール1から、正方形の面積=(半径×2)×(半径×2)÷2
正方形の面積=(半径×2)×(半径×2)÷2
正方形の面積=半径×2×半径
正方形の面積÷2=半径×半径
問題文などで正方形の面積が与えられていれば(よくあります)、
すぐに円の半径×半径(つまり半径)は分かるという事になります。
円と正方形のまとめ
1【円の中の正方形の面積は、その円の半径を1辺とする正方形の面積の2倍】
(円の半径×半径×2=正方形の面積)
2【半径×半径=円に内接する正方形の面積の半分】
(正方形の面積が与えられていれば円の半径(×半径)はすぐにわかる)

円と正方形の中学入試問題等
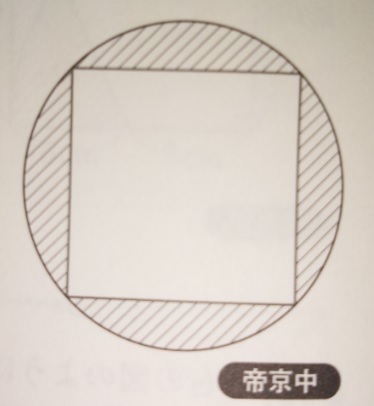
問題)帝京中学校
正方形の面積は18cm2です。円周率は3.14とします。
(1)正方形の対角線の長さは何cmですか?
(2)斜線部分の面積は何cm2ですか?
下記の問題集などで、飽きるほど問題を解きましょう。
頭で分かったつもりでも、体で理解しないと絶対に難問は
解けるようになりません。the more, the moreです。