
問題)1/6+1/12+1/20+1/30+1/42を計算しなさい
はい、こんな問題は「単位分数」のテクニックを知らなければ
「やりたくない」ですよね?でも、解法パターン・手続きを
知っていれば簡単にできます(下記に詳述)。
え?「単位分数」?何それ?ですよね?
大丈夫です。そこから説明します。
単位分数とは?分子が1の真分数のこと
単位分数とは分子が1の真分数のことです。
「分子が1」は良いとして「真分数」?ですよね?
真分数とは、分子が分母より小さい分数の事です。


出典:https://mathwords.net/shinbunsu
まとめると、
●分子が1
●真分数(分子が分母より小さい分数)
この二つの条件を満たすものが「単位分数」となります。
分子が1で分母が1ではなく2以上なら全て単位分数となる
という事になりそうですから、要するに
単位分数とは「分子が1の分数(分母は整数で2以上)」
と考えておいて良さそうです。
では、「単位分数」の何が大事なのか?
単位分数には法則があって、それを使わないと実質解けないような
中学受験の算数の問題がよくあるという事です。
単位分数の問題を解くテクニック2つ
単位分数のテクニック1:1/6=1/2-1/3
■単位分数のテクニック1■
分母(ex 6)が2つの連続する整数の積(2×3)で表せる単位分数は、
その連続する整数(2と3)を分母とする単位分数の差で表せる
注意点:分母が小さい方(分数としては大きい方)を前(先)に
実際の数字を見ないと分からないですよね・・・。
6=2×3
連続する整数の積で表せますので、
1/6=1/2-1/3
で表せるという事です。
逆に「連続する整数の積を分母とする単位分数」は
連続する整数を分母とする単位分数の差で表せると
考えてももちろんOKです。
3×4=12
ですから、
1/12=1/3-1/4
となるわけです。
そうなると、下記のような問題パターンが中学受験の算数では
出てきます。
例題)1/6+1/12+1/20+1/30+1/42を計算しなさい

分子がすべて「1」の時点で「単位分数のテクニック?」と
考えましょう。
6=2×3、12=3×4、20=4×5、30=5×6、42=6×7
ですね?
あとは、上記の図のような式が書ければ難しくはありません。
この種の単位分数の中学受験問題は、ある程度パターン化し
ていますので、この種の問題をたくさん解きましょう。
例題)桐蔭学園中学の入試問題
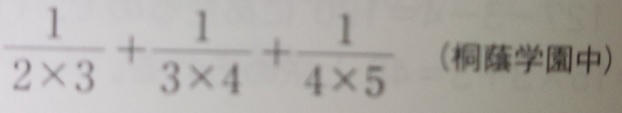
慣れてくると問題を見ただけで「あ、このパターンね。単位分数でしょ」となります。
単位分数の中学受験問題(東邦大附東邦中)
1/42+1/56+1/72+1/90 を計算しなさい。
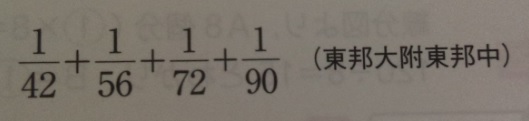
はい、このパターンね!ですね?
単位分数のテクニック2:2/15=1/3-1/5
■単位分数のテクニック2■
分母を2つの整数の積(ex. 3/10→3/2×5)で表した時、
【分子=分母の差】となる分数は、その2つの整数を分母
とする単位分数の差で表すことができる。
注意点:分母が小さい方(分数としては大きい方)を前(先)に
う~ん、日本語・文章だけでは分かりませんね・・・。
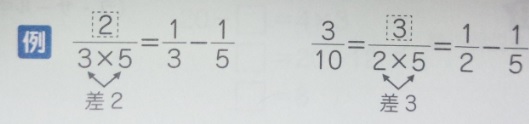
図を見ると分かりますでしょうか?
例題)芝中学

一度全て解ける必要はありませんが、一つ一つ解いていき、
何度かやって全て正解にできるようにしましょう。
単位分数の公式・テクニックを使わない(知らない)と、ほぼ
解けないでしょう・・・
まとめ:単位分数の問題を解く2つのテクニック!―「中学受験+塾なし」の勉強法
■単位分数のテクニック1■1/6=1/2-1/3
分母(ex 6)が2つの連続する整数の積(2×3)で表せる単位分数は、
その連続する整数(2と3)を分母とする単位分数の差で表せる
注意点:分母が小さい方(分数としては大きい方)を前(先)に
■単位分数のテクニック2■2/15=1/3-1/5
分母を2つの整数の積(ex. 3/10→3/2×5)で表した時、
【分子=分母の差】となる分数は、その2つの整数を分母
とする単位分数の差で表すことができる。
注意点:分母が小さい方(分数としては大きい方)を前(先)に