この記事では、図形の面積を求める際に必要な考え方・
テクニックを簡単にまとめます。
図形の公式等、平面図形の面積の基本については上記記事を
読んでください。ただし、この記事のレベルはまだ「基本」
となります・・・。とはいえ、基本を完璧にすれば、中学受験
の偏差値で55~60前後まではいけると思われます。
図形の面積の求め方のテクニック!―「中学受験+塾なし」の勉強法・教え方
1 分割する
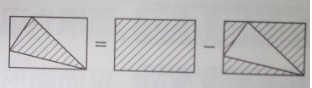
2 余分なところを引く
3 移動させる・変形する
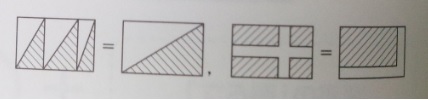
4 三角形の辺の比などを利用する
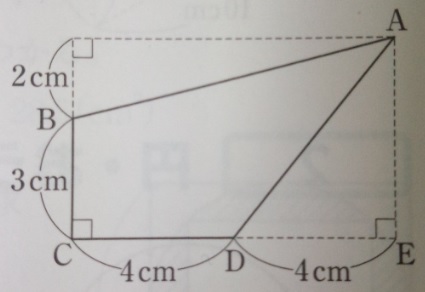
図形の面積の求め方のテクニック「1 分割する」

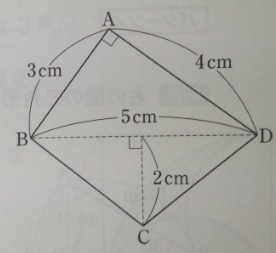
問題)上の図の四角形ABCDの面積は何c㎡ですか?
四角形を三角形二つに分割して解きます。
三角形ABDと三角形BCDになりますので、
(3×4÷2)+(5×2÷2)
=6+5
=11c㎡
図形の面積の求め方のテクニック「2 余分なところを引く」
上の図の四角形ABCDの面積は何c㎡?
点線を入れた四角形から二つの三角形を引く場合。
5×8=40c㎡
2×8÷2=8c㎡
4×5÷2=10c㎡
40-(8+10)=22c㎡
答え)22c㎡
台形ABCEから、三角形ADEを引く場合
(3+5)×8÷2=32
ADE=4×5÷2=10
32-10=22
答え)22c㎡
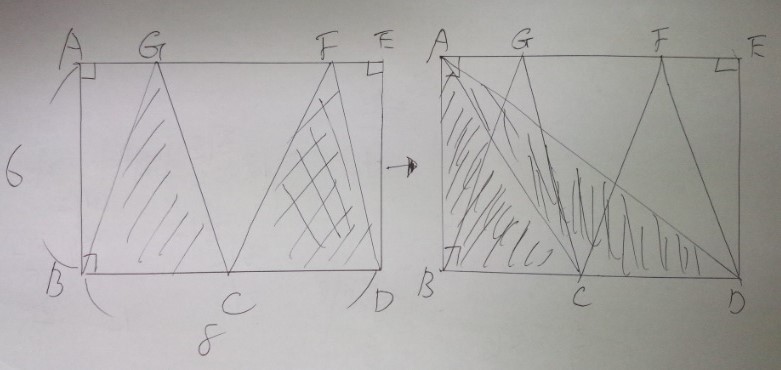
図形の面積の求め方のテクニック「3 移動させる・変形する」

問題)下記の左の図の斜線部分の面積の和は何c㎡ですか?

この形はある種のパターンですね。
三角形BCGと三角形CDFの面積が分かれば良いわけです。
三角形は「底辺」と「高さ」が分かれば面積は出ますので、
三角形BCG=三角形BCA
三角形CDF=三角形CDA
と変形させる事ができます(ここが一番のポイントです)。

となると、三角形BCG+三角形CDF=三角形ABD
である事がわかります。
底辺8×高さ6÷2=24
答え)24c㎡
「道路や花畑の面積」は「端に寄せる」のが基本
です。
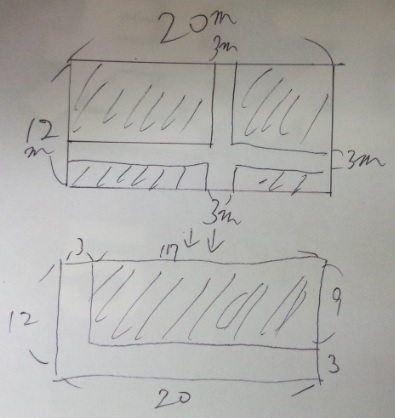
「斜線部分の面積を求めなさい。」といった類(たぐい)の問題です。
「道路や花畑の面積」は「端に寄せる」
17×9=153
答え)153㎡
ここまでシンプルに基本的な問題は中学受験ではまず出ませんが、
「端に寄せる」という考え方は難問でも同じです。
また、道路問題では「斜めになっている」ものがよくあります。
結論は「縦の長さにして良い」のですが、理屈を説明します。
ここで「斜めになってるから長さが5cmにならないのでは?!」と
思ったそこのあなた!素晴らしいですね。自分の頭で考えています。
伸びると思います。
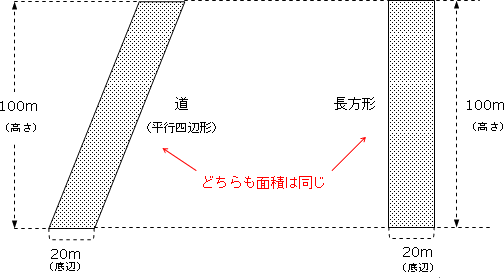
結論から言うと、「平行四辺形と長方形の面積は同じ」だから、
という事になります。なぜ同じか?公式で言うと、
平行四辺形=底辺×高さ
長方形=縦×横

このように「平行四辺形」はどんな形でも長方形に変形できるからです。
面積が同じなので、端に寄せてしまえるわけです。長さは違っても面積
が同じになるという事です。
例題)畑の面積を求めてください。
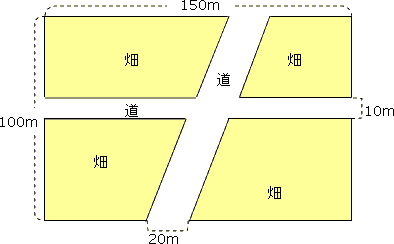
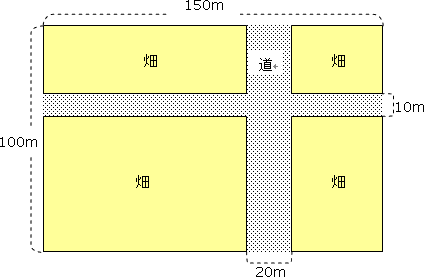
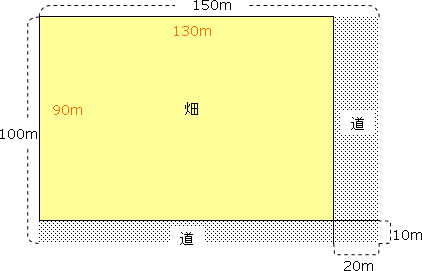
130×90=11700
答え)11700㎡
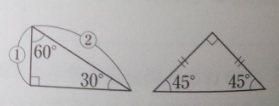
図形の面積の求め方のテクニック「4三角形の辺の比などを利用する」

問題)上の図の三角形ABCの面積は何c㎡?
30度、直角、45度といった角度を見たら「ピン!」と来ましょう。
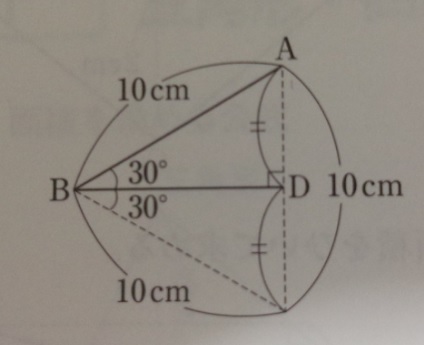
三角形ABDは正三角形を半分にしたものであることが分かります。
「30度」を見たら「二つあれば60で正三角形」と思いましょう。
となると、ADが5cmとすぐに分かります。
15×5÷2=37.5
答え)37.5c㎡?
まとめ
以上、
図形の面積の求め方のテクニック!(基本編)
でした。
基本ではありますが、このあたりを完璧にしておけば、「応用」にも
すぐに取り掛かれますし、そもそも難関中学であっても、「基本」の
徹底がもっとも有効な勉強法です。難関の場合、その後「応用」が
必要になりますが・・・。
再度まとめます。
1 分割する

2 余分なところを引く

3 移動させる・変形する

4 三角形の辺の比などを利用する

(関連記事)
