「歩数と歩幅」は「速さ」問題の一種です。
「速さ」の基本がまだかな?という方は先にそちらをお読みください。
言葉に慣れる事が大事かと思われます。
例題)だろう君が3歩で歩く距離を、びばりさんは4歩で歩きます。
また、だろう君が4歩歩く間に、びばりさんは3歩歩きます。
だろう君とびばりさんの歩く速さの比は、何対何ですか?
(解答・解説は下記で。え?ちんぷんかんぷん?大丈夫です、分かります)
「歩数と歩幅」問題は「面積図」か「線分図」を書くことで解けます。
個人的には「面積図」の方が分かりやすいので、そちらでいかせて頂き
ます。
「歩数と歩幅」問題の解き方は「面積図」を描く
例題)だろう君が3歩で歩く距離を、びばりさんは4歩で歩きます。
また、だろう君が4歩歩く間に、びばりさんは3歩歩きます。
だろう君とびばりさんの歩く速さの比は、何対何ですか?
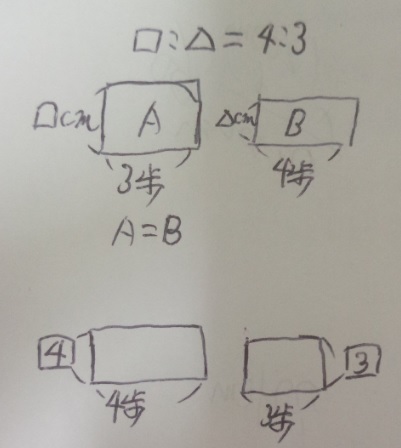
1 距離(歩数×歩幅)を面積で表します。

距離=歩数×歩幅 ですよね?
2人の歩数が分かっているので、面積図を書きます。
歩幅は分かりませんので、□と△にします。
AとBは同じですね?
という事は、□と△の比率は4:3になります。
だって、AとBの面積(距離)は同じなのですから。
2 歩幅の割合(4:3)と歩数の関係で面積図を作ります。
例題)だろう君が3歩で歩く距離を、びばりさんは4歩で歩きます。
また、だろう君が4歩歩く間に、びばりさんは3歩歩きます。
だろう君とびばりさんの歩く速さの比は、何対何ですか?
歩幅の割合が4:3と分かりました。

「歩幅の割合4×(だろうの)4歩=歩幅の割合3×びばりの3歩」ですね?
歩幅×歩数=距離です。
「速さと比」の基本で学びましたが、時間が同じなら、
速さの比がA:Bなら、距離の比はA:B
です。ですので、ともに距離を表しているので、
4×4:3×3
が、速さの割合でもあります。
答え)16:9
ちょっと分かりづらいですかね?問題をたくさん解いて慣れてください。
例題)だろう君が5歩で進む距離をびばりさんは6歩で進みます。
また、だろう君が10歩で進む時間でびばりさんは9歩進みます。
この時、だろう君とびばりさんの進む速さの比はいくつですか?
下記のような面積図が描けましたか?
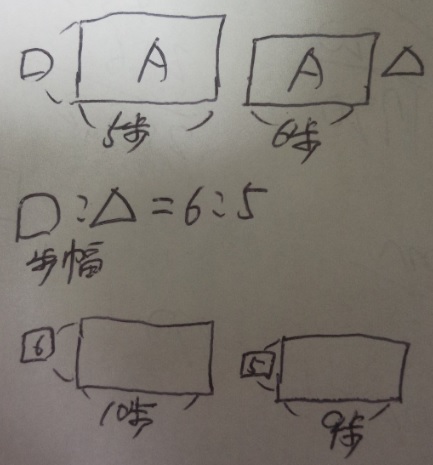
「速さと比」の基本で学びましたが、時間が同じなら、
速さの比がA:Bなら、距離の比はA:B
(6×10):(5×9)が速さの比になります。
60:45=4:3
答え)4:3
距離と速さの比の基本を頭に再度入れておきましょう。
(距離が同じ場合)
①速さの比がA:Bなら、時間の比はB:A
(速さが2倍なら、かかる時間は半分)
(時間が同じ時)
②速さの比がA:Bなら、距離の比はA:B
(速さが2倍なら、同じ時間進めば距離も2倍になる)
(速さが同じなら)
③距離の比がA:Bなら、時間の比はA:B
(速さが同じなら、距離が2倍になれば時間も2倍になる)
例題)京都の禅寺の最高位である南禅寺の周りで、だろう君とびばりさんが
ジョギングをしています。だろう君が2歩で走る距離を、びばりさんは3歩で
走ります。だろう君が3歩走る間に、びばりさんは4歩走ります。
だろう君は30分でゴールしました。びばりさんはゴールするのに何分何秒
かかるでしょう。
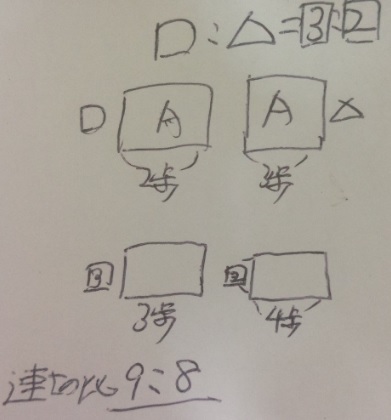
速さの比はだろう9:びばり8です。
ここで焦らないでください。速さの比がA:Bです、聞かれ
ているのは、かかった時間です。距離は同じです。
~~~~~~~~~~~~~~~~~~~~~
(距離が同じ場合)
①速さの比がA:Bなら、時間の比はB:A
(速さが2倍なら、かかる時間は半分)
(公式は下記を見てください)
https://bunpon.com/?p=1633#keni-toc6
~~~~~~~~~~~~~~~~~~~~~
距離が同じなら、
速い人(だろう君)の方がかかった時間はもちろん
短くなります。かかった時間の比は、速さの比をひっくり返して、
だろう8:びばり9
です。
8:9→30:?
8と30の関係は、8に30/8をかければ良いわけですから、
同じように、
9に30/8をかければ?がでますね?
9×30/8=270/8→135/4→33と3/4です。
何分何秒かかるか聞かれているので、分母を60にします。
です。33と45/60です。
答え)33分45秒
最初は難しく感じるかもしれませんが、慣れれば大丈夫です。
なお、「速さ」の基本がまだ身についていない場合は、
そちらを先に何度も何度も読んでください。