あります。
等差数列とは?
「数列」=数を(ある決まりによって)規則的に並べたもの
「等差数列」=(隣の数同士の)差が一定の数列
(差が一定=等差。その差の事を「公差」という)
「1 3 5 7 9 11~~~」(例・公差2の等差数列)
例題)6、10、14、18・・・・と規則的に増えていく数列
があります。はじめから数えて37番目の数はいくつですか?
(解答・解説は下記。公式・テクニックを知らないと、
「こりゃあかん・・」ですよね?大丈夫ですできます)
等差数列の解き方・テクニックは公式2つ!
□番目の数=1番目の数+公差×(□ー1)
1番目から□番目までの数の和=(1番目の数+□番目の数)×□÷2
*公式を忘れたら、簡単な等差数列を自分で作って数を当てはめてみると思い出しますよ
等差数列は基本問題に関しては、上記の公式が頭に入って
いれば解けます。
等差数列で□番目の数を求める問題の解き方
例題)6、10、14、18・・・・と規則的に増えていく数列
があります。はじめから数えて37番目の数はいくつですか?
最初の数は6、差(公差)は4ですね?
□番目の数=1番目の数+公差×(□ー1)
37番目の数=6+4×(37-1)
=150
公式を真に理解するには、公式に頼らない仕組み(公式の基に
なる部分)を知る事です。上記の問題であれば、
6 10 14 18 22
+4 +4 +4 +4
1番目の数=6+4×0=6
2番目の数=6+4×1=10
3番目の数=6+4×2=14
4番目の数=6+4×3=18
5番目の数=6+4×4=22
下線部分の数字は□番目の□から1を引いた数ですね?
□番目の数=1番目の数+公差×(□ー1)
となります。
*公式を忘れたら、簡単な等差数列を自分で作って数を当てはめてみると思い出しますよ
例題)1、4、7、10、13、16・・・という規則に従って数が
並んでいます。最初から数えて15番目の数はいくつですか?
□番目の数=1番目の数+公差×(□ー1)
15番目の数=1+3×(15-1)=43
答え)43
*公式を忘れたら、簡単な等差数列を自分で作って数を当てはめてみると思い出しますよ
例えば、2 4 6 8 10 12と作って、
3番目(6)は2+2×(3-1)=6
という感じですね。
□番目の数=1番目の数+公差×(□ー1)
1番目から□番目までの数の和=(1番目の数+□番目の数)×□÷2
*公式を忘れたら、簡単な等差数列を自分で作って数を当てはめてみると思い出しますよ
等差数列で□番目までの和を求める問題の解き方
「□番目までの和」を求めるには□番目の答えを出せる必要がある問題が多いです。
例題)6、10、14、18・・・・と規則的に増えていく数列
があります。はじめの数から37番目の数までを全て加えると、
その和はいくらになりますか。
□番目の数=1番目の数+公差×(□ー1)
37番目の数=6+3×(37-1)=150
答え)150
1番目から□番目までの数の和=(1番目の数+□番目の数)×□÷2
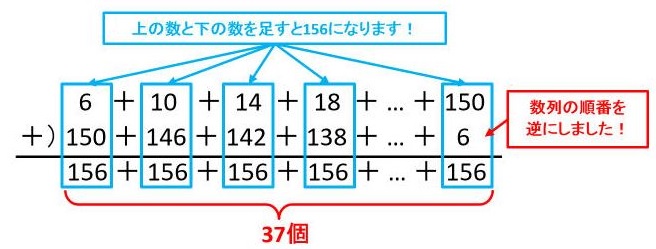
(6+150)×37÷2=2886
答え)2886
この公式は、図にすると、仕組み(公式の基になる部分)がある程度理解しやすいです。
画像出典:https://katekyo.mynavi.jp/juken/6856
例題)1、4、7、10、13、16・・・という規則に従って数が
並んでいます。最初から数えて1番目から20番目までの数の和は
いくつになりますか?
□番目の数=1番目の数+公差×(□ー1)
20番目の数=1+3×(20-1)=58
1番目から20番目までの数の和は、
(1+58)×20÷2=590
答え)590

1番目から□番目までの数の和系の問題の場合、上記のような
図を描いて見ると公式も思い出しやすいですし、そもそも「等差数列」の本質
に近いので、最初は図を描いた方が良いでしょう。
等差数列の中学入試問題等
問題)関東学院六浦中学
ある規則に従って、2, 5, 8, 11, 14, 17, 20・・・と整数が並ぶとき、
100番目の整数を答えなさい。
問題)13,15,17,19,21,…と規則正しく続く数列の251番目の数は?
問題)次の数列において、1767は何番目でしょう。
3,7,11,15,19,…
まとめ
以上、
等差数列の解き方・テクニックは公式2つ!
でした。
□番目の数=1番目の数+公差×(□ー1)
1番目から□番目までの数の和=(1番目の数+□番目の数)×□÷2
*公式を忘れたら、簡単な等差数列を自分で作って数を当てはめてみると思い出しますよ