
てこの基本:てこの原理!てこの3点!モーメントと逆比!3つ以上の力! この記事
てこの応用:支点が端にある(上と下に向かう力に分ける)・棒が曲がっている(垂直にして考える)
「てこ」の原理の基本
てこの原理とは?
「てこ」とは、小さな力で重いものを動かしたり、小さい力を大きな
運動(力)に変える道具です。
例えば、「シーソー」「はさみ」「ペンチ」「ピンセット」etc.
「てこ」を使った物理的な動きを「てこの原理」と言います。
ですから、
「てこの原理」とは、小さな力で重いものを動かしたり、
小さい力を大きな運動(力)に変える事と考えていいでしょう。
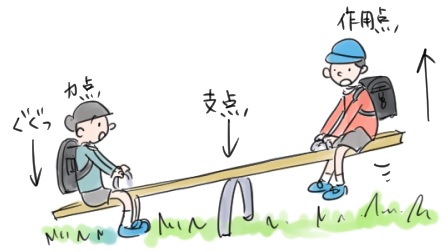
画像出典:https://kyoukasyo.com/2020/02/11/6science20/
てこの3点:支点・力点・作用点
【てこの3点】
1 支点:支えて動かない点
2 力点:力を加える点
3 作用点:加えた力が働く点
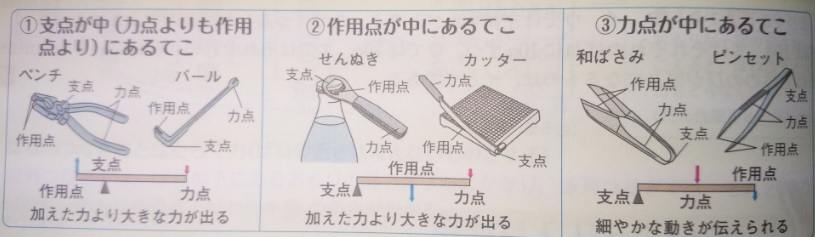
画像出典『塾技100理科』p66
図を見れば分かりますが、(道具の場合)「力点」が手で触る
(力を加える)ところですね。支点は動かないところです。
●楽に物を動かしたい場合:支点と力点の距離を長くします
支点と作用点の距離を短くします
物に大きな力を働かせたい場合、支点から力点までの長さが、
支点から作用点までの長さより長いほど良いという事です。
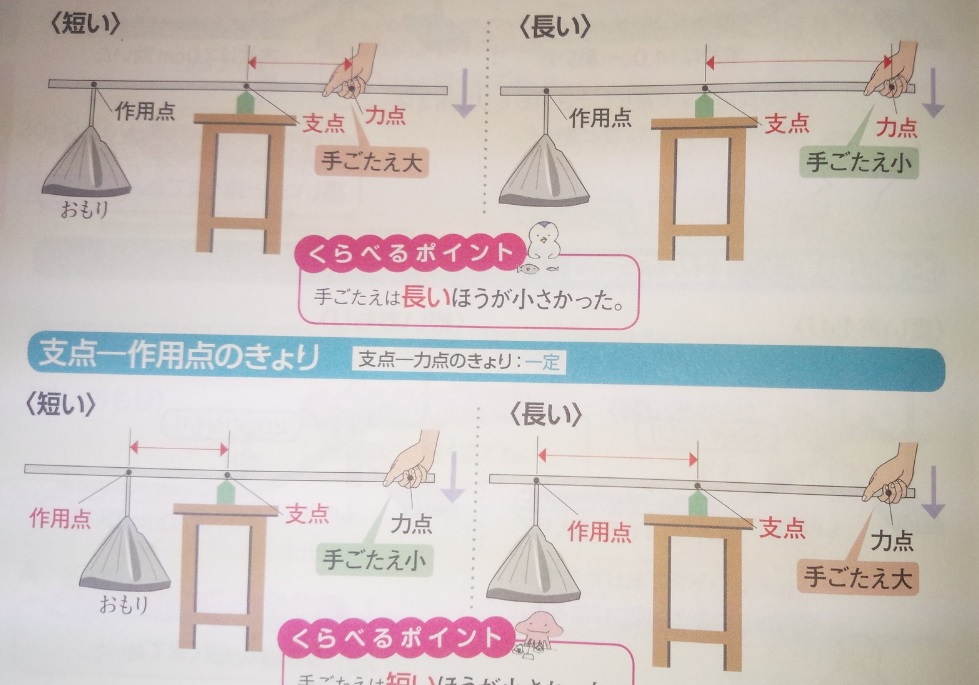
画像出典:『くらべてわかるできる子図鑑』p184
てこのつり合い:「モーメント」と逆比
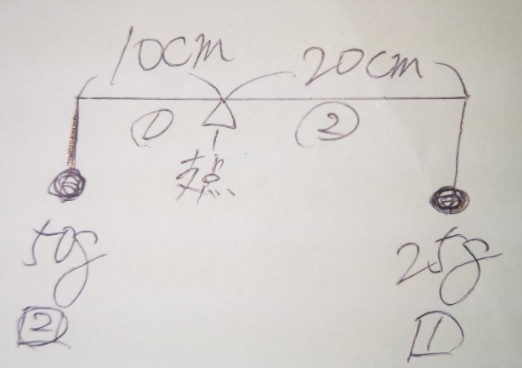
(左側)50×10=500 (右側)25×20=500
「おもりの重さ」×「支点からの距離」=モーメント
モーメントが同じだとつり合い、そうでなければ、
(当然)重い方に傾きます。
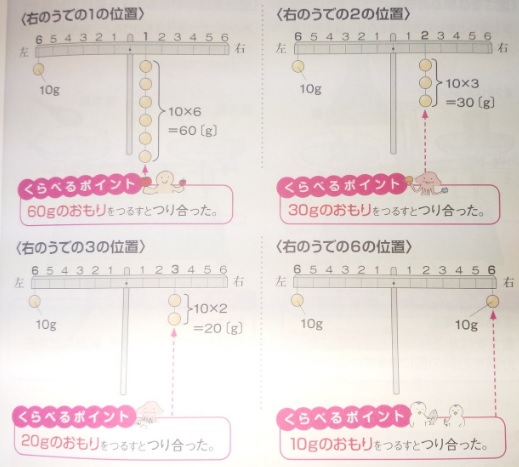
画像出典:『くらべてわかるできる子図鑑』p185
「おもりの重さ」(g)×「支点からの距離」(cm)が左右で同じだと釣り合う
(gとcmが多いですが、そうでない事もありえます)
(釣り合っている場合)「おもりの重さ」と「支点からの距離」は逆比
になりますので、そちらから計算する事もできます。

(釣り合っている場合)「おもりの重さ」と「支点からの距離」は逆比
つまり、上の図のように
おもりの重さが1:2なら、支点からの距離(うでの長さと言います)は2:1
になります。逆比ですね。
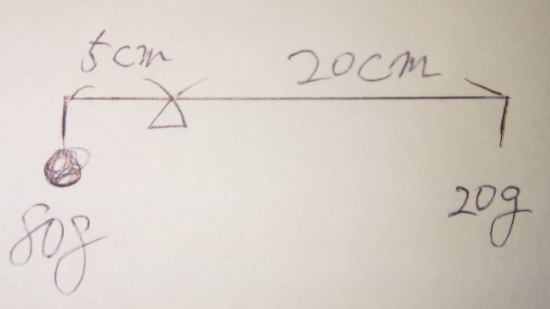
こちらの場合、80:20=4:1ですから、5:20=1:4になります。
(釣り合っている場合)「おもりの重さ」と「支点からの距離」は逆比
になります。
てこがつりあうとき、力が2つなら逆比とモーメントで、力が3つ以上
ならモーメントを使いましょう。
3つ以上の力でつりあう時の問題の解き方
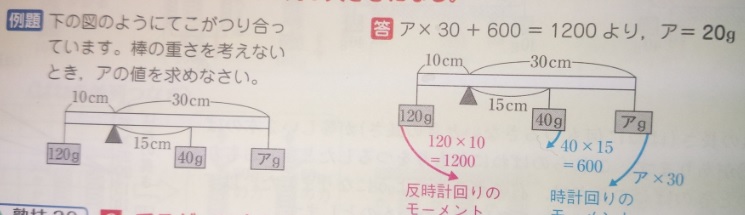
画像出典『塾技100理科』p66
1 釣り合っている所で求められるおもりの重さを求める
2 1でわかった物を利用して残りのおもりの重さを求める
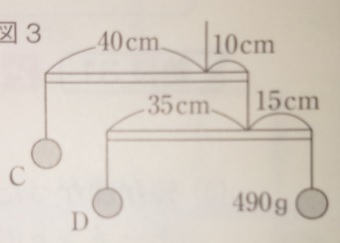
(明治大学付属中野八王子中学の入試問題より抜粋)
問題)CとDのおもりの重さを求めてください。

まず、2つの力だけで釣り合っているDが求められそうです。
35×D=15×490, 35×D=7350, D=210
次にCです。
うでの長さの比は4:1ですから、力の比は1:4になります。
「4」がD(210)+490です。
「4」=700
700÷4=175
「1」=175 C=175g
答え)C175g, D210g

支点にかかる力(上向きの力)
(つりあっているとき)支点にかかる力(上向きの力)と下向きの力は等しくなります。
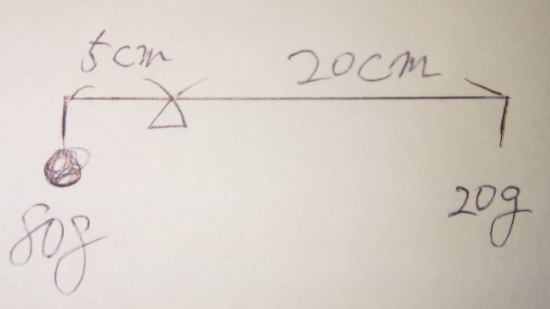
この図であれば、支点には80g+20g=100gの力がかかります。

この図であれば、50g+25gで75gですね。
棒に重さがある場合
問題によっては、「棒に重さ」があります。
●棒の重さは、重心(棒の中心の事が多いがそうでない事もある)にあると考えます
●(中心までの距離-釣り合っている点までの距離)×棒の重さ=棒の重さが働く力
●棒に重さがある場合、「棒の重さ」もモーメントとして考える必要があります。
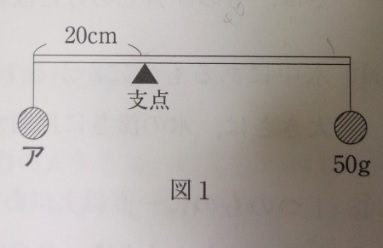
問題)国府台女子学院中学
図1のように棒の左端から20cmのところに支点を置き、右端に50gの
おもりを吊り下げました。棒を水平にするために左はしに吊り下げた
おもりは何gですか?
なお、棒の長さは60cm、重さは120gです。

考え方)棒の重さもモーメントに入れて考える必要があります。
●棒の重さは、重心(棒の中心)にかかる=中心以外で釣り合っていれば棒の重さもそれに関係する
●(中心までの距離-釣り合っている点までの距離)×棒の重さ=棒の重さが働く力
●棒の重さが働くのは中心よりも長い方だけ
時計回りに働く力(モーメント)は、棒の重さの傾き+おもりによる力
(30-20)×120+(50×40)=1200+2000=3200g
3200÷20=160
答え)160g
*「重心」=中心とは限りません(めんどくせ~~・・・)
重心の位置は物の形によって決まります。

●太さが同じなら重心=中心
●太さが同じでない場合、重心は左右の端をばねばかりでつるした重さの逆比

まとめ
●「てこの原理」とは、小さな力で重いものを動かしたり、
小さい力を大きな運動(力)に変える事と考えていいでしょう。
●【てこの3点】
1 支点:支えて動かない点
2 力点:力を加える点
3 作用点:加えた力が働く点

画像出典『塾技100理科』p66
物に大きな力を働かせたい場合、支点から力点までの長さが、
支点から作用点までの長さより長いほど良い

画像出典:『くらべてわかるできる子図鑑』p184
「おもりの重さ」×「支点からの距離」=モーメント
モーメントが同じだとつり合い、そうでなければ、
(当然)重い方に傾きます。

画像出典:『くらべてわかるできる子図鑑』p185
「おもりの重さ」(g)×「支点からの距離」(cm)が左右で同じだと釣り合う
(釣り合っている場合)「おもりの重さ」と「支点からの距離」は逆比

(3つ以上の力で釣り合っている時のおもりの重さの求め方)
1 釣り合っている所で求められるおもりの重さを求める
2 1でわかった物を利用して残りのおもりの重さを求める

一回だけだと混乱するかもしれないので、何度もこの記事を読んで練習しましょう。
てこの基本:てこの原理!てこの3点!モーメントと逆比!3つ以上の力! この記事
てこの応用:支点が端にある(上と下に向かう力に分ける)・棒が曲がっている(垂直にして考える)