三角数は1番目の数が1、公差1の「等差数列の和」/公式：（1＋ｎ）×ｎ÷2―「中学受験＋塾なし」の勉強法!

（関連記事）

（基本）等差数列の解き方・テクニックは公式2つ！

四角数は二乗＋1から始まる連続した奇数（1＋3＋5＋7＋9…）の和!

三角数とは？

「三角数」？知らんがな！ですよね？

そうすると、次は、1＋2＋3＋4＋5＝15ですね？

これは「等差数列」の考え方とほぼ同じです。

ですが、「等差数列」の公式は、

【1番目から□番目までの数の和＝（1番目の数＋□番目の数）×□÷２】

書き方が違うだけで全く同じですね？例えば下記の右端。

n番目の三角数：（1＋ｎ）×ｎ÷2：（１＋４）×４÷2＝１0

【1番目から□番目までの数の和＝（1番目の数＋□番目の数）×□÷２】

（1＋4）×4÷2＝10

ですから、「三角数」＝1番目の数が1、公差1の「等差数列の和」の事と言えます。

 

三角数の公式・n番目の三角数：（1＋ｎ）×ｎ÷2

すでに書きましたが、三角数の公式は以下です。

問題）7番目の三角数はいくつ？

n番目の三角数：（1＋ｎ）×ｎ÷2

（１＋７）×7÷2＝28　答え）28

 

良く出てくる三角数：「45」と「55」

良く出てくる三角数：「45」と「55」。これは暗記ですね。

1＋2＋3＋4＋5＋6＋7＋8＋9＝45　（1＋9）×９÷2＝90÷2＝45

1＋2＋3＋4＋5＋6＋7＋8＋9＋10＝55　（1＋10）×10÷2＝110÷2＝55

問題）下記のパターンで数字が並んだ場合、10段目の一番右はいくつ？

全部書く！という事も可能ですが…入試だと時間なくなります。

「三角数」（もしくは等差数列）なので、（1＋10）×10÷2＝55　答え）55

 

三角数（の公式：（1＋ｎ）×ｎ÷2）の中学入試問題等

問題）和洋九段女子中学

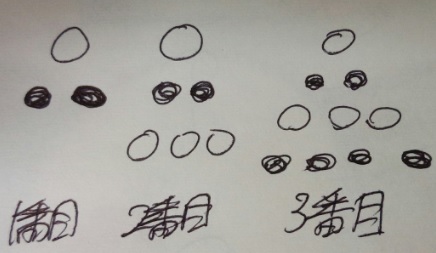
図のように白と黒のご石を正三角形になるように並べます。

（１）6番目の正三角形にはご石が全部で何個ありますか？

（２）1辺のご石の個数が9個の時、この正三角形には白のご石が全部で何個？

（３）正三角形を作る白のご石の個数が黒よりも11個多いのは何番目の正三角形？

解法）（１）6番目の正三角形にはご石が全部で何個ありますか？

１）書いてもそんなに速さがかわらなそうですね…

２）「三角数の公式」：（1＋6）×6÷2＝21　ですが・・・・この問題は1番目が

すでにご石3個なので、通常の三角数で言う所の「2番目」です。

３）ここでは「6番目」＝「三角数の7番目」になりますので、（1＋7）×7÷2＝28

答え）28個

 

解法）（２）1辺のご石の個数が9個の時、この正三角形には白のご石が全部で何個？

１）1辺9個なので、ご石の数は：（1＋9）×9÷2＝45

２）図を書いた方が早いでしょう　

1＋3＋5＋7＋9＝25　答え）25個

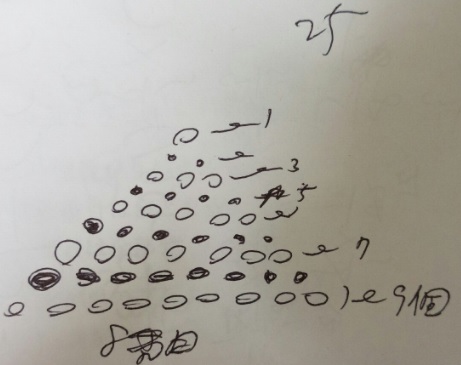
（３）正三角形を作る白のご石の個数が黒よりも11個多いのは何番目の正三角形？

１）白の方が多くなるのは偶数番目

２）2番目が4：2（差２），4番目が9：6（差３）、差が1個ずつ増えていくので、

6番目（差４）、8番目（差５）、10番目（差６）、12番目（差７）、14番目（差８）、

16番目（差９）、18番目（差10）、20番目（差11）

たぶん、地道に数えるのが一番速いです。

答え）20番目

 

問題）共立女子中学　この規則で並んでいる場合

（１）11段の中央の数は？

（２）70は第何段の左から何番目？

解法）（１）11段の中央の数は？

１）書いた方が速いかも・・・

２）61ですね

３）もちろん【「三角数」が左右順番に出てくる】ことを利用してもOK

奇数段の三角数は左側、11段＝（1＋11）×11÷2＝132÷2＝66

４）11段目は数字が11個なので中央は66から数えて5番目、1ずつ減るので61

（書いた方が速そう）

解法）（２）70は第何段の左から何番目？

１）66が11段目の左端→12段目の左が67

２）12段目：６７、６８、６９、７０

３）答え）第12段目の左から4番目

答え）（１）61　（２）第12段目の左から4番目

 

まとめ

（関連記事）

（基本）等差数列の解き方・テクニックは公式2つ！

四角数は二乗＋1から始まる連続した奇数（1＋3＋5＋7＋9…）の和!