
(関連記事)
三角数は1番目の数が1、公差1の「等差数列の和」/公式:(1+n)×n÷2
「四角数」を理解するには「三角数」について先に読んでください。
四角数とは?

「四角数」?知らんがな!ですよね?
四角数は
●「四角数」=平方数:同じ整数を2乗したもの●(ex.9は3×3なので3の平方数)
●1から始まる連続した奇数(1+3+5+7+9…)の和●
●碁石などを四角形に並べた時の総数が名前の由来
●「四角数」=1番目の数が1、公差2の等差数列の和
(「三角数」=1番目の数が1、公差1の「等差数列の和」)
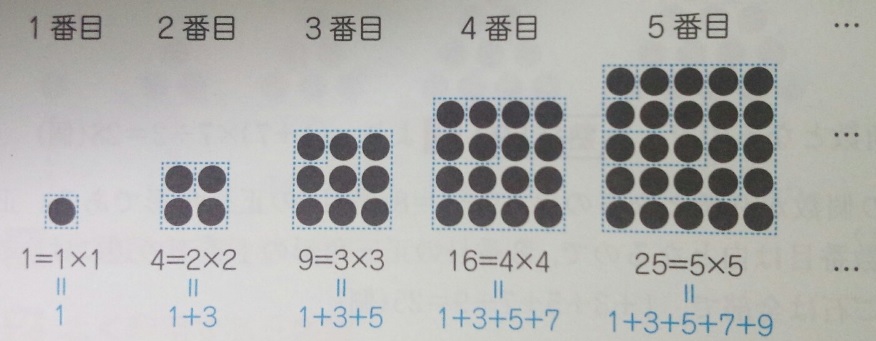
出典:『塾技100算数』p186
そうすると、次は、36 =6×6(1+3+5+7+9+11)ですね?
四角数の公式
n番目の四角数=n×n
です。ちなみに、
【1番目から□番目までの数の和=(1番目の数+□番目の数)×□÷2】(等差数列)
n番目の三角数:(1+n)×n÷2(三角数)
でしたね?


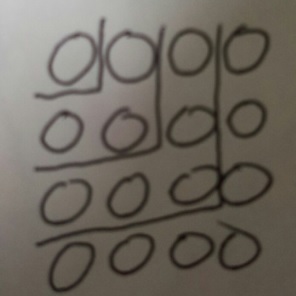
上下どちらかから書くかは問題によりますが、この数字のパターン=四角数です。
左のように区切ると、奇数の和が1+3+5+7=16と右の図で分かりますよね?
四角数=三角数のとなりどうしの和
三角数と四角数の関係は、
【四角数=三角数のとなりどうしの和】
です。見るのが一番早いでしょう。
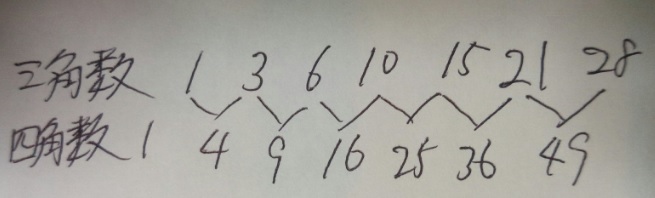


三角数 四角数
問題)下記のパターンの場合、10段目の一番左の数は?

解法)
1)右端の数字が「四角数」(1の二乗、2の二乗、3の二乗…)と見抜くのが大事
2)10段目なら右端は10×10=100、ただ求めるのは左端…
3)9段目の右端+1=10段目の左端なので、9×9=81、81+1=82
答え)82


上下どちらかから書くかは問題によりますが、この数字のパターン=四角数です。
左のように区切ると、奇数の和が1+3+5+7=16と右の図で分かりますよね?
四角数は二乗!(2×2、3×3、4×4…)の中学入試問題等
問題)豊島岡女子学園中学
奇数の和が1+3+5+7は下の図を用いて16と求める事が
できます。この考え方を用いて1から99までの奇数の和を求めてください。

解法)一見難しいですが、冷静にやりましょう
1)1から始まる連続した奇数(1+3+5+7+9…)の和=四角数
なので、「四角数」を使います
2)7までの奇数の和が16なのは、図で端の○が7個あるからですね?4×4
3)という事は、99までの奇数は、図の端の○が99個になればOKです。
7が3+3+1なので、99は49+49+1という配置になります。
4)という事は「縦」「横」ともに50です。
5)50×50=2500
答え)2500
*もっとシンプルに、99は(99+1)÷2=50番目の奇数と考えても良いです。
問題)共立女子中学
規則に沿って左下から番号がついています。左から○個、
下から□個の所にあるのを(○、□)と表します。例えば
8番は(3,2)。
(1)(6,3)は何番?
(2)111番はどのように表せますか?

解法)(1)(6,3)は何番?
1)下段の1,4,9,16,25を見てすぐに「あ、四角数」と気づきましょう
2)(左から6,下から3)なので、下段は36ですね。下から3つめなので、34
(問題文の次の列ですから、念のため書いてみることをオススメします)
答え)34
解法)(2)111番はどのように表せますか?
1)111という事は、10×10=100、11×11=121ですから、101~121がある、
11×11の所、つまり11列目ですね
2)11列目だけ書きましょう。5列目が縦4、横4、角1ですから、11列目は縦10横10、角1

3)111は角です。なので(11、11)
答え)(11、11)
答え)(1)34、(2)(11、11)
まとめ
四角数は
●「四角数」=平方数:同じ整数を2乗したもの●(ex.9は3×3なので3の平方数)
●1から始まる連続した奇数(1+3+5+7+9…)の和●
●碁石などを四角形に並べた時の総数が名前の由来
●「四角数」=1番目の数が1、公差2の等差数列の和
(「三角数」=1番目の数が1、公差1の「等差数列の和」)

出典:『塾技100算数』p186


上下どちらかから書くかは問題によりますが、この数字のパターン=四角数です。
左のように区切ると、奇数の和が1+3+5+7=16と右の図で分かりますよね?
四角数のもんだいの多くは上記の図のパターンが出ますので、そしたら、
「四角数」!とピンと来てください。
(関連記事)
三角数は1番目の数が1、公差1の「等差数列の和」/公式:(1+n)×n÷2