(関連記事)
てこの基本:てこの原理!てこの3点!モーメントと逆比!3つ以上の力!
てこの応用:支点が端にある(上と下に向かう力に分ける)・棒が曲がっている(垂直にして考える)
組み合わせかっ車・輪じく(りんじく)(じくと輪にかかる力の比は、それぞれの半径の逆比)
輪じく(りんじく)はてこの原理+じくと輪にかかる力の比は、それぞれの半径の逆比
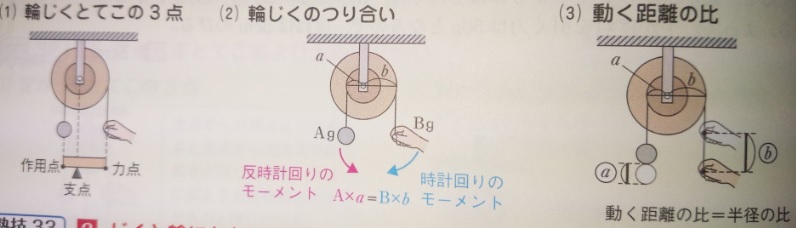
輪じく(りんじく):半径の小さい軸(中心)に半径の大きい輪を組み合わせて回転するようにした物
小さい力で大きな力を生み出せる=てこの原理。ドアノブ、ハンドル、蛇口など
輪じくはてこの原理です。「てこをかたむけるはたらき=おもりの重さ×支点からの距離」でしたが、
てこの基本:てこの原理!てこの3点!モーメントと逆比!3つ以上の力!
輪軸は、「輪軸を回すはたらき=おもりの重さ×輪の半径」となります。
また、てこでは、「左にかたむけるはたらき=右にかたむけるはたらき」でした。
右の力と左の力が同じであればつり合うということになるわけです。
これに対して、輪軸では、「左に回すはたらき=右に回すはたらき」となります。

画像出典『塾技100理科』p72
(2)の図から、下記が成り立つ。
A×a=B×b→A(おもり):B(引く力)=b(輪):a(じく)
じくと輪にかかる力の比は、それぞれの半径の逆比となる
組み合わせかっ車
組み合わせかっ車の問題は、ひもが1本でつながっているかつながっていないかで
解き方が変わります。
かっ車が1本のひもでつながっている場合
画像出典『塾技100理科』p72
かっ車が1本のひもでつながっている場合
おもりの重さ+動かっ車の重さ
1)ひもを引く力=――――――――――――――――
動かっ車を支えるひもの数
2)ひもを引く距離=物体の移動距離×動かっ車を支えるひもの数

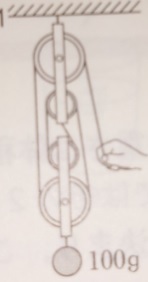
画像出典『塾技100理科』p72, 73
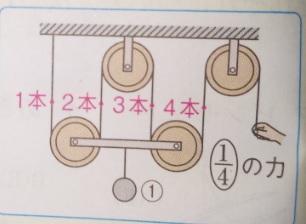
上の図の場合、(かっ車の重さを考えずに)つりあわせる場合、動かっ車を支える
ひもの数は4本なので、100+0/4=25 25gの力でひもを引けばつりあいます。
かっ車が1本のひもでつながっていない場合
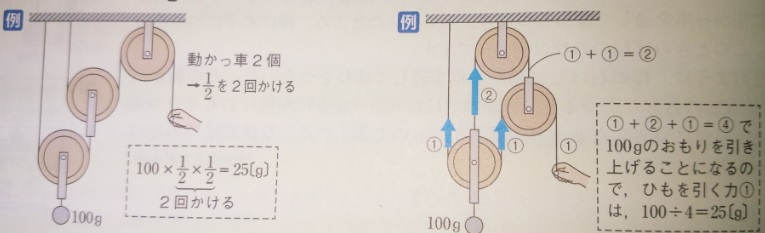
かっ車が1本のひもでつながっていない場合にひもを引く力を求める方法2つ
1)おもりの重さに動かっ車の数だけ1/2をかける
(定かっ車は数に入れません)
2)ひもを引く力を①としてそれぞれのひもにかかる力を表す
【ひもを引く距離】は仕事の原理を使うので、ひもを引く力が1/4倍になると、
ひもを引く距離は4倍になる。
~~~~~~~~~~~~~~~~~~~~~~~
仕事量:物を動かすために使った力と動かした距離との積
同じ「仕事」をする場合、道具を使っても使わなくても仕事量は変わらない(仕事の原理)
~~~~~~~~~~~~~~~~~~~~~~~~~~~~
(関連記事)
てこの基本:てこの原理!てこの3点!モーメントと逆比!3つ以上の力!
てこの応用:支点が端にある(上と下に向かう力に分ける)・棒が曲がっている(垂直にして考える)
組み合わせかっ車・輪じく(りんじく)(じくと輪にかかる力の比は、それぞれの半径の逆比)