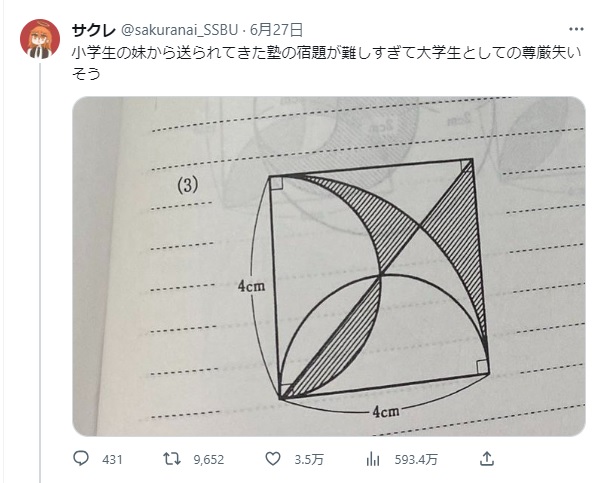
twitterで話題の算数の問題を解説しますが、鍛えられている
小学生だと本当に10秒くらいで答えます。
等積移動の典型パターン問題

斜線部分の面積を求めよという問題ですね。
中学受験+算数では必須のパターンです。
【等積移動の典型パターン問題】
1 「等積移動」を知っているか問われていると気付く
2 「どこをどう移動させるか」考える+(必要なら)補助線引く
3 「移動」させる
4 計算する
これだけです。

答え:4cm²
ですね。鍛えられている小学生だと本当に10秒くらいで答えます。
先に大事な事を言います。
こういうのは「パターン」なので教えられてる子は10-60秒くらいで解ける。解法を教えられてない子はどんだけ地頭❓良くても解くのに時間がかかるか解けない。それが中学受験。課金勝負?ある意味そう。決まったパターンをどれだけ知っていてどれだけ早くこなせるか。
— 塾なしで中学受験するブログ→できました。 (@bunponcom) June 28, 2023
こういうのは「パターン」なので教えられてる子は10-60秒
くらいで解けます。解法を教えられてない子はどんだけ地頭?
良くても解くのに時間がかかるか解けません。
それが中学受験です。課金勝負?ある意味そうですね。
決まったパターンをどれだけ知っていてどれだけ早くこなせるか
の勝負です。
(関連記事)
図形を解く工夫:等積移動・共通部分の利用―「中学受験+塾なし」の勉強法!
【等積移動の典型パターン問題】
1 「等積移動」を知っているか問われていると気付く
2 「どこをどう移動させるか」考える+(必要なら)補助線引く
3 「移動」させる
4 計算する
具体的な「解法」としてはこの図になりますね。
斜線部分は、四角形全体の面積の4分の一という事が分かります。

4×4×1/4=4
答え:4cm²
「補助線を引く」に加えて、
●同じ面積の所を移動させる●(等積移動)
というものを覚えてください。
理屈としては、等積移動は、そのままでは面積を求めづらい問題を解く
ために、図形の一部を移動させ、おうぎ形や三角形、四角形を作って
面積を求めます。
文字で書かれても???ですよね?図を見て理解しましょう。
ある程度パターン化されているので、何度もやっていると覚えてしまえ
ます。
また、中学受験の算数入試問題レベルになると、等積移動させないと、
あるいはパターンを知らないと(少なくとも時間内には)解けない問題
というのが基本になっていたりします・・・。世知辛い世の中ですね。
【等積移動の典型パターン問題】
1 「等積移動」を知っているか問われていると気付く
2 「どこをどう移動させるか」考える+(必要なら)補助線引く
3 「移動」させる
4 計算する
まとめ
こういうのは「パターン」なので教えられてる子は10-60秒
くらいで解けます。解法を教えられてない子はどんだけ地頭?
良くても解くのに時間がかかるか解けません。
それが中学受験です。課金勝負?ある意味そうですね。
決まったパターンをどれだけ知っていてどれだけ早くこなせるか
の勝負です。
逆に言うと、こういう問題を「0から考えて解く」というのは
時間が限られている受験では勝負になりません。
自分が知っている「パターン」なのかどうかをまず考えるのです。
もしくは頭の引き出しを探すんです。

4×4×1/4=4
答え:4cm²
なければ「捨て問」です。
もちろん、「地頭」の良い子なら、10分~20分と考えれば解ける
かもしれませんが、パターンをたたき込まれている子が10秒で解い
ている間に10-20分使っていたら全体ではどうなるかという話です。
合格するのは「頭」が良い子ではなく、パターンをたたき込まれてい
る子という事になります。
それが受験です。
(関連記事)
図形を解く工夫:等積移動・共通部分の利用―「中学受験+塾なし」の勉強法!
中学受験の算数のパターンが網羅されている「塾技」では、等積移動は
p72に載っています。