倍数判定法(2,3,4,5,6,8,9,10,11,12)/算数・youtube音声動画付き
ここでは、「最小公倍数」と「最大公約数」を使う
典型的なパターンの問題に慣れておきたいと思います。
そのためには、「最小公倍数」と「最大公約数」の基本が
完璧でなければいけませんので、下記関連記事を未読の方
は先に読んでください。
図形の切り分け系問題:最大公約数と最小公倍数を使う
二つ以上の図形を切り分けて、「最も大きく(最大公約数)」「最も
小さく(最小公倍数)」する系の問題です。
●(最初はきちんと)図を描いてみる
●1辺が最も大きくなるように→最大公約数
●1辺が最も小さくなるように→最小公倍数
問題)縦30cm、横45cmの長方形を、できるだけ大きな正方形に
切り分ける時、
(1)正方形の1辺は何cmにすれば良いですか?
(2)また、その時、何枚の正方形ができますか?
考え方)正方形は長方形より小さくなるので、最大公約数を使います。
30と45の最大公約数は、3×5=15
3)30 45
5)10 15
)2 3
(1)答え)15cm
(2)また、その時、何枚の正方形ができますか?
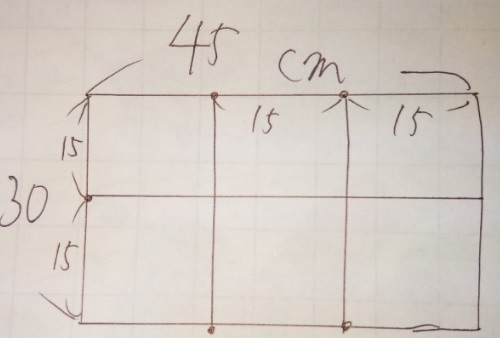
(2)答え)6個
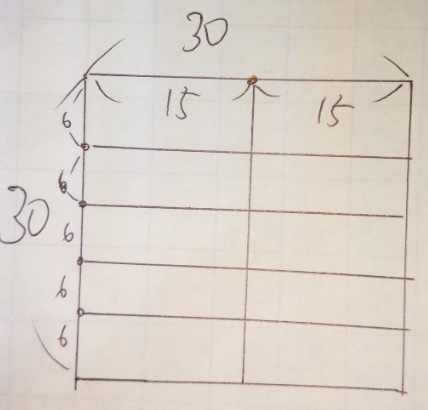
問題)縦6cm、横15cmの長方形の板をすきまなく並べて、
できるだけ小さい正方形をつくります。
(1)この正方形の1辺は何cmにすればよいですか。
(2)その時、この板は何枚必要ですか?
考え方)「できるだけ小さい正方形」なので、最小公倍数ですね?
3)6 15
2 5
3×2×5=30 30が最小公倍数。
●(最初はきちんと)図を描いてみる

(1)30cm (2)10枚
問題)栄東中学校
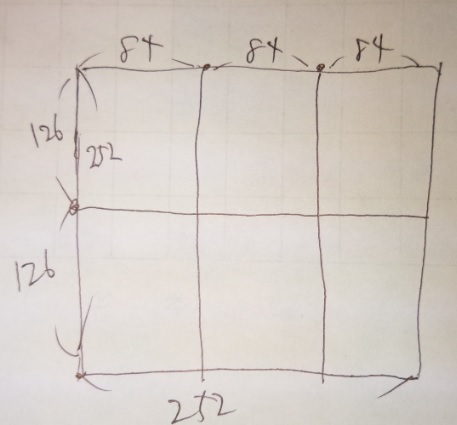
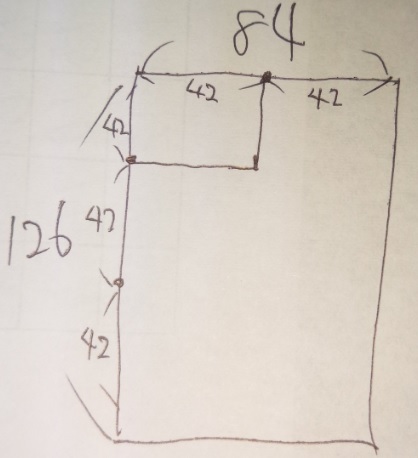
縦の長さが126cm、横の長さが84cmの長方形のタイルがあります。
(1)このタイルを敷きつめて正方形を作る時、最低□枚必要です。
(2)このタイルをあまりを出さないように、最も大きい同じ大きさの
正方形に切り分けた時、正方形の1辺の長さは□cmです。
「~~がともに整数」系問題:【分母の最小公倍数/分子の最大公約数】
【B/A×○/□とD/C×○/□がともに整数になる○/□は?】
【分母の最小公倍数/分子の最大公約数】
(AとCの最小公倍数/BとDの最大公約数)
例)8/15と12/25にかけてともに整数になる最小の分数は?
分母の最小公倍数=75
分子の最大公約数=4
答え)75/4
8/15×75/4=10 12/25×75/4=9
理由)
8/15×○/□=整数
12/25×○/□=整数
なので、○は15と25の公倍数でなければなりません。
同じように□は8と12の公約数でなければなりません。
「最小」なので、分子は最小公倍数となり、分母は
最大公約数となります。
理由を理解できればいちばん良いですが、
【B/A×○/□とD/C×○/□がともに整数になる○/□は?】
【分母の最小公倍数/分子の最大公約数】
(AとCの最小公倍数/BとDの最大公約数)
を公式として覚えてしまっても良いかと思います・・・。
問題)4/5と8/9の両方にかけてどちらも整数となる最も小さい分数を求めてね
このパターンの問題の公式は
【分母の最小公倍数/分子の最大公約数】
ですので、
分母5と9の最小公倍数:(割れないので)45
分子4と8の最大公約数:4
答え)45/4=11と1/4
なお、数字(分数)が3つ以上になっても考え方は同じです。
問題)4と2/3、8と3/4、8と1/6にかけてどれも整数となる最も小さい分数を求めてね
(星野学園中学)
考え方)まず、仮分数に直しましょう。
14/3 35/4 49/6
ですね。
【分母の最小公倍数/分子の最大公約数】
分母の最小公倍数 12
2)3 4 6
3)3 2 3
1 2 1
2×3×2=12
分子の最大公約数 7
7)14 35 49
2 5 7
12/7→1と5/7
答え)1と5/7
倍数判定法(2,3,4,5,6,8,9,10,11,12)/算数・youtube音声動画付き