
受験は「差」をつける競技です。出題される中で、他の子ができない、
もしくは時間がかかる所を、「できる」「速くできる」にしておくだ
けでかなりの「差」がつきます。
いやらしい話ですが、その「差」の積み重ねが偏差値の差になります。
この記事では、そういった中学受験で差がつくもののなかで、
「算数の計算の工夫・コツ・テクニック」
をまとめています。詳細は別途記事を紹介しています。
これらのものが出てきたら、
「あ~はいはい」と思いながら、テクニックを使って処理して
しまいましょう。
レベルとしては「中学受験では必須」位なので、必ず覚えましょう。
中学受験の計算の工夫・コツ・テクニックはこの6つ!算数で必須!
1 二桁の二乗は暗記・語呂合わせで覚える(11×11~19×19)
2 円周率の倍数は暗記する!
3 交換法則と結合法則
4 分配法則(計算の工夫)/a×b+a×c=a×(b+c)
5 小数と分数の変換
6 2桁の掛け算は「分解」して暗算しろ!25×36は?
1 二桁の二乗は暗記・語呂合わせで覚える(11×11~19×19)
(詳細記事はこちら)
「二桁の二乗」というのは、11×11とか13×13など、二桁の
同じ数字の掛け算の事です。
下記の「二桁の二乗」は暗記必須です。
計算問題(それ以外も)を解くスピードに大きな差がつきます。
九九ができない、遅いというのは受験以前の問題なので、あまり
差がつきませんが、それが二桁になっただけで大きな差がつきます。
■2桁の2乗の暗記・語呂合わせ■
11×11=121(語呂合わせ「いいいいいにいい:良い良い胃に良い」
12×12=144(語呂合わせ「12月はイシシ」)
13×13=169(語呂合わせ「いざ、いちろー君!」)
14×14=196(語呂合わせ「いよいよひとくろう」)
15×15=225(計算方法あり!★ 5 × ★ 5 = (★+1) × ★ の後ろに25をつける!)
16×16=256(語呂合わせ「いろいろにこむ」)
17×17=289(語呂合わせ「い~な、二泊」)
18×18=324(語呂合わせ「いやいや、ミニよ」)
19×19=361(語呂合わせ「行く行く、さむい!」)
「二桁の二乗」は暗記必須
(詳細記事はこちら)
2 円周率の倍数は暗記する!
(詳細記事はこちら)
中学受験では「円周率は3.14で計算してください」という場合が
ほとんどです。
3.14は有名な数字なので、誰でも知っています。
でも、それが半分になったり、3倍、5倍となるとどうでしょう?
知っているかどうかだけで「差」がつきます。
■円周率の倍数(黄色数字を見たらピンと来ること)■
3.14×1/10(0.1)=0.314
3.14×1/5(0.2)=0.628
3.14×1/4(0.25)=0.785
3.14×1/2(0.5)=1.57
3.14×2=6.28
3.14×3=9.42
3.14×4=12.56
3.14×5=15.7
3.14×6=18.84
3.14×7=21.98
3.14×8=25.12
3.14×9=28.26
3.14×25(5×5)=78.5
3.14×36(6×6)=113.04
(詳細記事はこちら)
計算問題などで「3.14」が出てきたら、周囲に、その倍数等が
ないかを注意するだけで全然違います。
0.785
1.57
6.28
12.56
等は頻出です。
【3倍+0.14倍!】
円周率の倍数は暗記するといっても、何も考えずに丸暗記しろとはいいません。
逆にそれは効率が悪いです。
「3.14」という事は、「3倍と少し」です。
下記の数字はすべて「3倍と少し」ですよね?
3倍はすべて暗記しているはずですので、0.14の方を計算するなり、繰り返し
くっつけるなりの練習をしていると自然と覚えていけるかと思われます。
3.14×2=6.28 3×2=6
3.14×3=9.42 3×3=9
3.14×4=12.56
3.14×5=15.7
3.14×6=18.84
3.14×7=21.98
3.14×8=25.12
3.14×9=28.26
3.14×25(5×5)=78.5
3.14×36(6×6)=113.04
「3.14」という事は、「3倍と少し」ですので、トンチンカンな
数字にだけはならないようにしましょう。
ここまで読んでくれた方のために、多少ずるいですが、確率的には
けっこう高い、
「円周率関連のわからない問題の答えの当て方」
を教えます。解き方ではなく「当て方」です。
問題の中に「円」「円周率」が出てきて、答えが分からない場合、
知っている円周率の倍数を解答欄に書いてください。
体感としては、3~8分の一で正解になります。
この辺りの数字を答えにしている問題が多いかな…。
3.14×4=12.56
3.14×5=15.7
3.14×6=18.84
3.14×7=21.98
3.14×8=25.12
うちの子にはこの「ずるい技」を教えていましたが、模試なんか
では、ほぼ毎回1か所くらいはあったようですよ。
そのうち、3~8回に一回当たれば確率高いですよね?しかも算数は
一問の配点が高いし…。
■円周率の倍数(黄色数字を見たらピンと来ること)■
3.14×1/10(0.1)=0.314
3.14×1/5(0.2)=0.628
3.14×1/4(0.25)=0.785
3.14×1/2(0.5)=1.57
3.14×2=6.28
3.14×3=9.42
3.14×4=12.56
3.14×5=15.7
3.14×6=18.84
3.14×7=21.98
3.14×8=25.12
3.14×9=28.26
3.14×25(5×5)=78.5
3.14×36(6×6)=113.04
(詳細記事はこちら)
3 交換法則と結合法則
交換法則・結合法則!たし算・引き算・掛け算・割り算の計算の工夫・算数/youtube音声動画付き
●交換法則:たし算と掛け算は順番を交換しても答えは同じ:4+5=5+4、3×5=5×3
a+b=b+a
●結合法則:たし算と掛け算はどこで結合(かっこをつけても)させても答えは同じ
3+5+6=(3+5)+6=3+(5+6)、
2×3×5=(2×3)×5=2×(3×5)
a×b=b×a
例題) 92+43+57
これはすべてたし算なので、順番を変えても答えは変わりません。
慣れてくるとパッと見て、「あ、これは100になるな」と分かる
わけですが・・・。先に、43+57=100を計算して、
92+100=192
この記事の交換法則と結合法則の記事のYouTube動画です。
交換法則・結合法則!たし算・引き算・掛け算・割り算の計算の工夫・算数/youtube音声動画付き
複数の引き算が混じる場合のポイントは、
引く数を足し合わせて計算する事ができる
点です。
例題)128-64-36
128から、「64」と「36」を引くので、
128-(64+36)=128-100=28
引き算の場合、単純に計算の順番を変える事はできません。
上記の例で言えば、128-(64-36)といった形に
変えると答えが違ってしまいます。
例題) 358-69-58
「358」と「58」が計算しやすそうな顔をしてますね?
「358-58-69」としても答えは同じです。
300-69=231
例題)173-140+127-160+368-100
こういう問題が出た場合、
「どことどこをくっつけたら分かりやすい数字になるか」
と考えながら解くのがポイントです。
まず、たし算は順番を変える事ができます。
引き算が複数ある場合は、引く数を足し合わせて計算する
事ができるでしたね?
では、考えてみてください。
例題)173-140+127-160+368-100
はい良いですか?
答え)(173+127)-(140+160)+368-100=300-300+368-100=268
「どことどこをくっつけたら分かりやすい数字になるか」
がポイントです。
慣れてきたら、以下のような問題は暗算でもできるはずです。
例題)3400-7800+6600
答え 10000-7800=2200
たくさん問題を解いて、交換法則・結合法則に慣れる事が
大事です。
交換法則・結合法則!たし算・引き算・掛け算・割り算の計算の工夫・算数/youtube音声動画付き
4 分配法則(計算の工夫)/a×b+a×c=a×(b+c)
(詳細記事はこちら)
分配法則(計算の工夫)/a×b+a×c=a×(b+c)・算数/youtube音声動画付き
この記事のyoutube音声動画です。
いきなり「分配法則」と言われても分からないと思いますが、
「算数の計算をする際の工夫」
と考えれば大丈夫です(そもそも名前に意味はありません)。
ポイントは
【たし算と掛け算は順番を入れ替えても答えが変わりません】
です。
例題)8.42×24+1.58×24-5×24
こんな問題を前から正直やってたら時間が足りません。同じ数字(ここでは24)
を見たらピンと来ましょう。
8.42×24+1.58×24-5×24
=(8.42+1.58-5)×24
=5×24
=120
ポイントとしては
「「24」という同じ数に三つの数をかけているので、
それを「分配」して計算をしやすくする事ができる」
というテクニックがあるという事を覚えましょう。
こういった種類の計算問題は中学入試では頻出です。
●計算問題で1つの式に同じ数がいくつかあったら分配法則を使う可能性が高いです●
a×b+a×c=a×(b+c)
8×10+8×2=8×(10+2)=96
a×b+a×c=a×(b+c)
このタイプの分配法則はかなりたくさん出てきますので、同じ数字がいくつか
出てくる計算問題があったら、「これは分配法則を使えって事かな?」と
ひらめく(受験的ではありますが・・・)センスが大事です。
極端に言うと、「分配法則」系の中学入試問題は、ほぼ全て、上記の基本
法則の応用(バリエーション)と考える事もできます。
図で見てみると分かりやすいかもしれません。
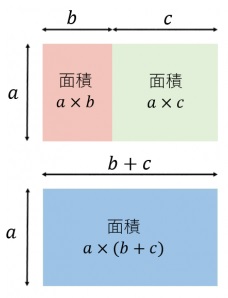
また、上の例は逆に考えると、二桁と一桁のかけ算は無意識に分配法則を
使っているという事でもあります。
12×8=(10+2)×8=8×10+8×2=96
この式を右から逆に辿れば分配法則の計算になります。
a×b+a×c=a×(b+c)
です!
算数(数学)ですから、(人生と違って・・・)公式にどんな数字を
入れても答えは必ず出ます。
a×b+a×c=a×(b+c)
2×12+2×9=2×(12+9)=2×21=42
例題)67×18+12×67
答え)67×(18+12)=67×30=2010
こういった問題を分配法則を使わずに、正面から正直に
解いてはいけないのでしょうか?
中学受験としてはダメでしょうね。時間がかかりすぎますし、
そもそも、問題を出す側は「分配法則を使えますか?」という
事を聞いていますので・・・。
それに、とても便利なので「分配法則」を覚えて使えるように
しましょう。
分配法則の割り算は(a+b)÷c=a÷c+b÷cは成立しますが、
a÷(b+c)=a÷b+a÷cは成立しません。
例題)525÷6-225÷6 (お茶の水女子大付属中)
答え)(525-225)÷6=50
これ位の問題であれば、「あれ、これは分配法則を使って良い割り算だっけ?」
と思ったら、頭から計算してもそんなに時間は変わらないかもしれません。
525÷6=87.5、225÷6=37.5 87.5-37.5=50
(詳細記事はこちら)
分配法則(計算の工夫)/a×b+a×c=a×(b+c)・算数/youtube音声動画付き
5 小数と分数の変換
(詳細記事はこちら)
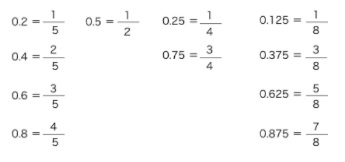
算数の計算問題で必須なのが、
分数と小数の変換
です。これが頭に入っていると計算問題を解くのが速くなります。そうすると、他の
問題に時間を割けますし、そもそも「計算ミス」が減ります。良い事しかありません。
以下は暗記してすぐに出てくるようにしましょう。
1/2⇔0.5
1/4⇔0.25
2/5⇔0.4
3/5⇔0.6
3/4⇔0.75
4/5⇔0.8
1/8⇔0.125
3/8⇔0.375
5/8⇔0.625
7/8⇔0.875
小数、分数どちらからも変換できるようにしましょう!
実は下二けたが[25][75]が多いので意外と覚えやすいです。
黄色マーカーは差がつきやすいです。
1/8(0.125)は1/4(0.25)の半分で1/4(0.25)は1/2(0.5)の半分
ですから意外と論理的でしょ?
上記がマスターできたら、次はこちらを。
0.02⇔1/50
0.04⇔1/25
0.08⇔2/25
0.96⇔24/25(96/100)
1.25⇔5/4
1.375⇔11/8
1.4⇔7/5
1.5⇔3/2
2.5⇔5/2
0.05⇔1/20
0.025⇔1/40
1.125⇔9/8
黄色マーカーが完ぺきだとかなり「差」がつきます。
やり方は、小数と分数どちらかだけを書いた紙を
大量に用意して問題演習!問題演習!問題演習!
全て「瞬間的に答えが出てくる」までやりましょう。
当然、分数と小数どちらからも変換できるのが大事です。
(詳細記事はこちら)
6 2桁の掛け算は「分解」して暗算しろ!25×36は?
「25×36は?」
下記を読むと、この問題を暗算で10秒で解けるようになります。
中学受験の算数では、
「基本的な計算」(四則演算:たし算、掛け算、割り算、引き算)
をいかに正確に速くできるかがとても大事になります。
(「正確に」が先です。その次に「速く」)
●2桁の掛け算は「分解」しろ!●
「分解」すると「暗算」できます。
実例を示すのが速いでしょう。
15×18=270
ですが、これを正直にやると時間がかかります。
計算しやすく「分解」して考えます。
18=2×9なので、
15×18=15×2×9
30×9=270
25×36ではどうでしょう?
25×4×9ですね?
25×36=25×4×9
(25×4=100は人生においても大事なので暗記しておいてね)
25×36=900
これは、中学校で習う「因数分解」というものの応用なのですが、
小学生であればそれは知らなくても良いです。良いですが、
36=4×9
や
25×4=100
こちらは、「正確に速く」できる必要があります。
そして、それらを組み合わせると、
25×36=900
15×18=270
などの計算が「正確に速く」できますので、是非積極的に
活用してください。
●2桁の掛け算は「分解」しろ!●
です。
下記の問題を暗算でスッとできるようになればなかなか良い感じです。
(暗算で15秒くらいだと素晴らしいです)
例題
(2.5×1.4)+3½+0.35 は?
(3½は3と½です)
答え
2.5×1.4=2.5×2×0.7=3.5
3½=3.5
3.5+3.5=7
7+0.35=7.35
まとめ
1 二桁の二乗は暗記・語呂合わせで覚える(11×11~19×19)
2 円周率の倍数は暗記する!
3 交換法則と結合法則
4 分配法則(計算の工夫)/a×b+a×c=a×(b+c)
5 小数と分数の変換
6 2桁の掛け算は「分解」して暗算しろ!25×36は?
中学受験の算数は、
「正確に速く」
計算をできるだけでかなり差がつきます。
上記の6つの
「中学受験の計算の工夫・コツ・テクニック」
をマスターしていると、「速さ」が圧倒的に違います。
是非!
(関連記事)
交換法則・結合法則!たし算・引き算・掛け算・割り算の計算の工夫・算数/youtube音声動画付き
分配法則(計算の工夫)/a×b+a×c=a×(b+c)・算数/youtube音声動画付き
分配法則(計算の工夫)/a×b+a×c=a×(b+c)・算数/youtube音声動画付き


