関連記事)
過不足算とは?
過不足算は、余りや不足から全体の差を考えて、
個数や人数を求める問題です。「差集め算」と似ています。
例えばこんな問題です。
「みかんがいくつかあります。これを家族で分けます。一人2個ずつ
分けるとみかんは7個余り、5個ずつ配ると5個足りませんでした。
このときみかんは何個ありますか?」
「差集め算」と同じ公式が使えます。
全体の差÷1個当たりの差=個数
です。
過不足算の解き方のテクニック:図表を描く
「差集め算」と同じく「図表」を正確に描ければほぼ問題は
解けます。
上記の問題であれば図表は以下のようになります。
「みかんがいくつかあります。これを家族で分けます。一人2個ずつ
分けるとみかんは7個余り、5個ずつ配ると5個足りませんでした。
このときみかんは何個ありますか?」

全体の差÷1人(個)当たりの差=個数(人数)
全体の差は「7個余りと5個不足」なので12個となります。
1人あたりの差は5-2で「3」個です
ですので、全体の人数(個数)は12÷3=4人ですね。
検算してみましょう、4×2+7=15、5×4-5=15
あっていますね。
答え)15個
注意点:「全体の差」を出す時は以下の点に注意が必要です。
A個余る、B個余る
⇒全体の差は A-B
A個不足、B個不足
A個余る、B個不足⇒全体の差は A+B
「余る(+)」と「足りない(-)」はなので、それこそ
理屈で考えて間違えないようにしましょう。
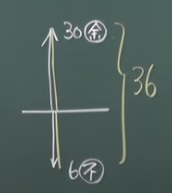
(基本の仕組み、考え方は「差集め算」と同じです)
全体の差÷1人(個)当たりの差=個数(人数)
過不足算の中学入試問題等
例題)
いちごがいくつかあります。これを家族でひとり2個ずつ分けるといちご
は7個あまり、5個ずつ配るとは1個あまりました。
このときいちごは何個ありますか?
例題)
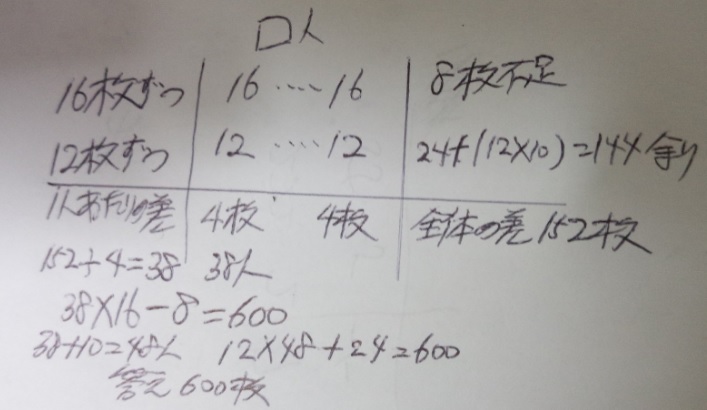
何人かの子供に1人16枚ずつカードを配ったところ8枚足りませんでした。
10人の子供が加わったので、今度は1人12枚ずつ配ったところ24枚余り
ました。カードは全部で何枚ありますか?(明治大学附属明治中学)
中堅校~難関校の中学受験問題は「基本パターンにひとひねり」加えている
ものがほとんどです。ですので、最初はできなくても良いかと思いますので、
もし図表を描いてみたけど、できない!ムキ~~~~!!!という場合は、
答えを見てもいいです。そのかわり、もう一回、もう2~5回やってみて、
完全に自分で正答まで導けるようにしましょう。
(関連記事)