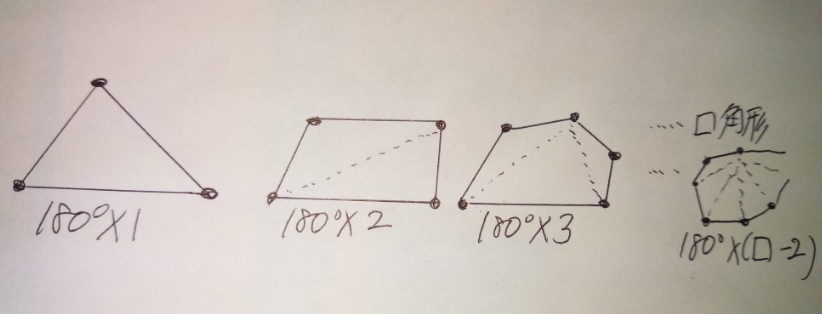
(関連記事)
角度2:多角形の内角の和=180°×(□角形-2)/多角形の外角の和は360°
多角形の内角の和=180°×(□角形-2)
多角形の外角の和は360°
角度の問題を解く時には、これを体の覚えるレベルで知っている
と解くスピードが速まると思います。
多角形の内角の和=180°×(□角形-2)
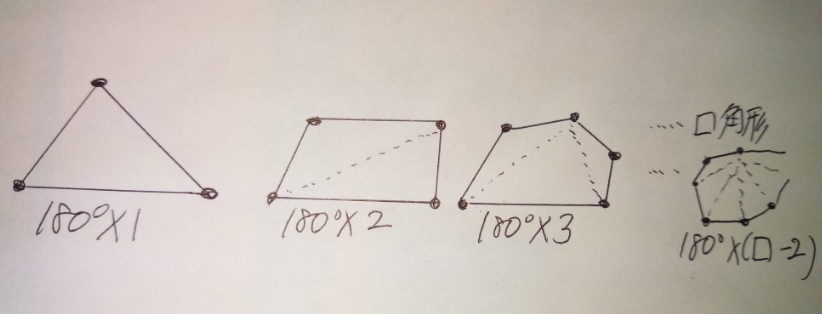
多角形の内角の和=180°×(□角形-2)です。
五角形(540°)くらいまでは暗記しているかと思いますが、
理屈で知っておくとよりいいでしょう。
三角形の内角の和が180°で、それをもとにすると、四角形では
(一つの頂点から)三角形が2つでき、五角形では3つという
感じですね。
多角形の対角線の数の公式((頂点の数ー3)×頂点の数÷2)
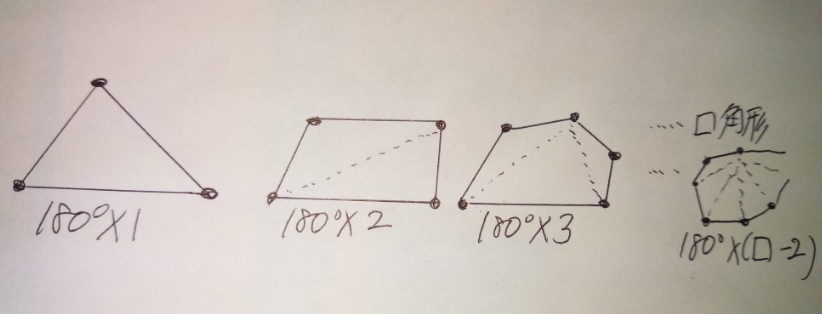
なお、上記の考え方(多角形の一つの頂点から対角線を引いて
三角形に分ける)は「対角線の数」にも使えます。
多角形の「対角線の数を求めなさい」というタイプの問題には
以下の公式が使えます。
(頂点の数ー3)×頂点の数÷2
【●1つの頂点からひける対角線の数と頂点の数を掛けて(重なり部分の)2で割る●
という仕組みです。】
忘れたら三角形、四角形など分かりやすいものの
数字を入れて考えましょう。
三角形の対角線の数
(頂点の数3ー3)×頂点の数3÷2=0
四角形の対角線の数
(頂点の数4ー3)×頂点の数4÷2=2
五角形の対角線の数
(頂点の数5ー3)×頂点の数5÷2=5
六角形の対角線の数
(頂点の数6ー3)×頂点の数6÷2=9
多角形の外角の和=360°
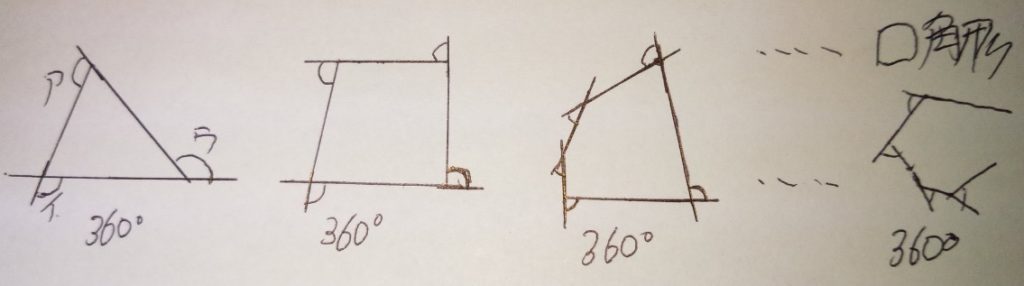
すべての
多角形の外角の和は360°
です。
上記のルールを知ったら、後は問題集などで大量に角度の
問題を解いてみてください。
解く時は紙に印刷するなり、自分で書くなりして、必ず図形に
分かる角度等を書き込むようにしましょう。頭だけでは解かない
こと。何しろ、体で覚える事が大事ですから。
角度の問題例題
問題)下記の図の「A」の角度は何度ですか?
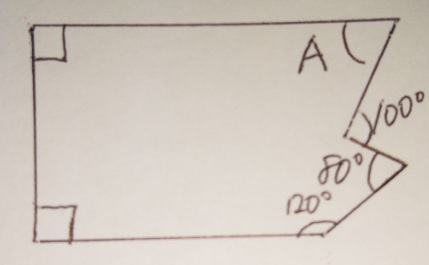
考え方)
どうも「多角形の内角の和」っぽいですね。
多角形の内角の和=180°×(□角形-2)
6角形なので、内角の和は「180×(6-2)=720°」
後はそれ以外の内角の和を720°からひいていきましょう。
直角が2つ(180)
120と80で200
外角が100°なので内角は360-100=260
これで全部ですね?
180+200+260=640
720-640=80
答え)80度
問題)下記の図の「ア」の角度は何度ですか?(城北中学入試問題)

多くの問題集にあたってたくさん飽きるくらい問題を解きましょう。
(関連記事)
角度2:多角形の内角の和=180°×(□角形-2)/多角形の外角の和は360°