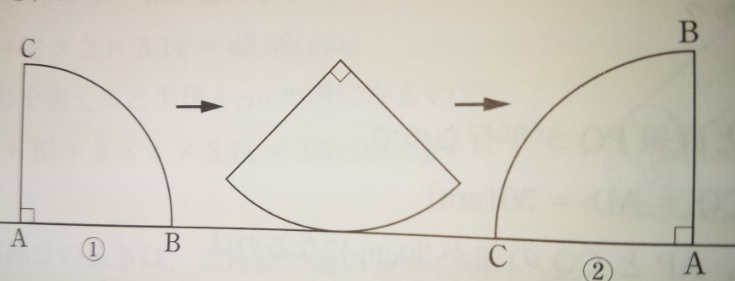
回転する三角形や四角形〔図形)のポイント
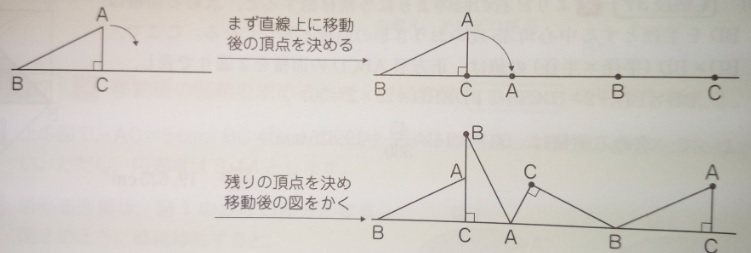
出典:『塾技100算数』p82
1)1点だけ移動後の頂点を直線上に決める
2)直線上にない残りの点を決める
3)弧を描きながら移動する:同じ点をおうぎ形で結ぶ
3)〔回転する多角形の図を書くのに)慣れる

出典:『塾技100算数』p83
図が書けたら、同じ点を弧〔おうぎ形)に結ぶと移動した
ルートになります。
問題)1辺の長さ6cmの正三角形ABCが直線上をすべらない
ように一回転します。点Bが動く道のりは何cmですか?
円周率は3.14です。〔市川中学)

最初は図を書くのに慣れましょう。
1)1点だけ移動後の頂点を直線上に決める
2)直線上にない残りの点を決める
3)弧を描きながら移動する:同じ点をおうぎ形で結ぶ
3)〔回転する多角形の図を書くのに)慣れる
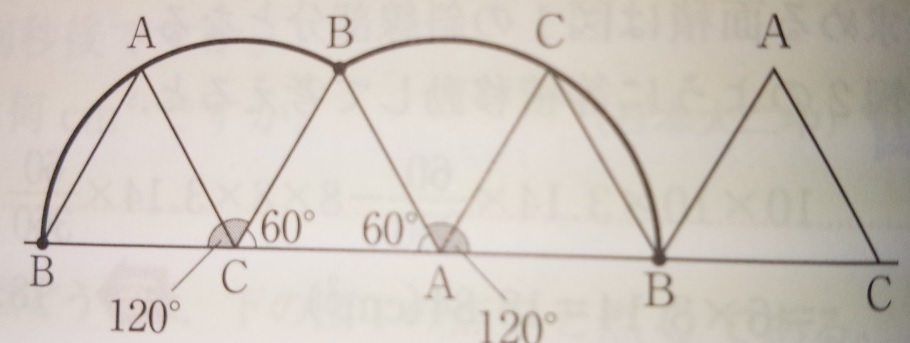
正三角形なのですべての角度が60度です。
弧を描きながら移動する
のがポイントです。
半径6cm、中心角120度のおうぎ形の弧が2つですね。
(6+6)×3.14×120/360×2
=8×3.14
=25.12
答え)25.12cm
回転するおうぎ形(図形)のポイント
上記のYouTube動画が分かりやすいです。
おうぎ形が回転する際のポイント!
1)おうぎ形の半径と同じ半径の中心角90度のおうぎ形が2つ(左と右)
2)真ん中の四角の上下の長さは(転がる)おうぎ形の弧と同じ長さ
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
中心が描く線は【「「中心角90度」のおうぎ形の弧」×2+直線】になる。
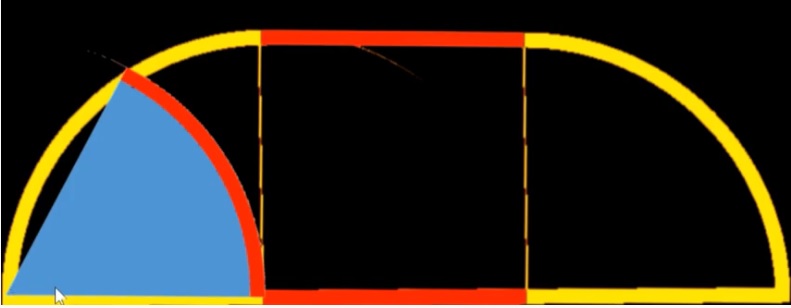

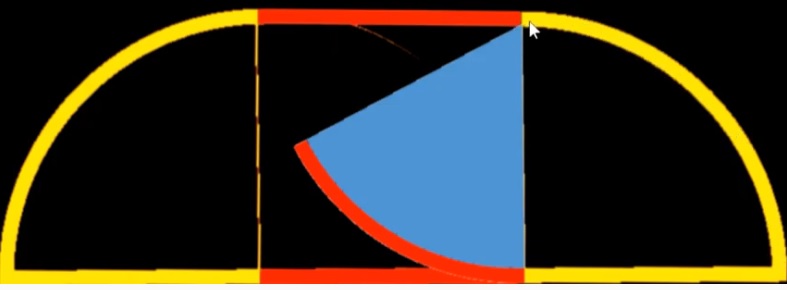

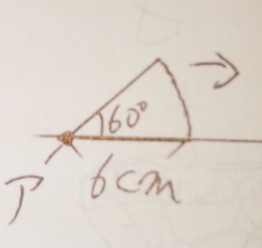
問題)下記の図のように、半径6cm、中心角60度のおうぎ形が、
矢印方向に床を一回転するとき、点アの動いた長さを求めてください。
円周率は3.14です。
おうぎ形が回転する際のポイント2つ!
1)おうぎ形の半径と同じ半径の中心角90度のおうぎ形が2つ(左と右)
2)真ん中の四角の上下の長さは(転がる)おうぎ形の弧と同じ長さ
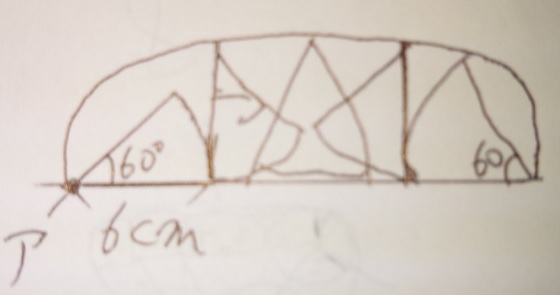
ですので「ア」が移動する長さは
1)中心角90度で半径6cmのおうぎ形の弧×2
2)半径6cm、中心角60度のおうぎ形の弧
になります。
〔(6+6)×3.14×90/360×2〕+(6+6)×3.14×60/360
=(12×3.14×1/4×2)+(12×3.14×1/6)
=6×3.14+2×3.14
=(6+2)×3.14
=25.12
答え)25.12cm
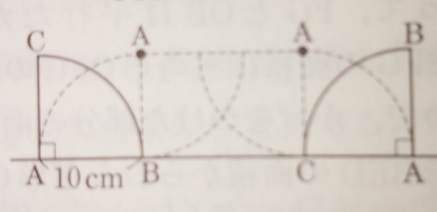
問題)栄光学園中学
半径10cm、中心角90度のおうぎ形です。
図①から図②になるまで転がしたら点Aが動いた道のりは何cmですか?