おうぎ形の面積の求め方2つと葉っぱ(レンズ)形の面積の求め方3つ!
ひもを巻きつけた図形・円の長さは「直線」と「曲線」に分ける!
図形の周りをひもが回っていく場合の考え方(つながれた犬が動ける面積)
図形の移動:平行移動のテクニック
1 移動の作図の場合「1点ずつ」動かす
2 両方動いている時は「差」を使う(片方止める):1秒ごとに何cm動くか
(追いかける形の場合「追いつき算」)
3ぶつかる形の場合は両者の「和」の速さで動く(「出会い算」)
(ぶつかる形でも「片方止めて」考えるのは有効です)
4 重なり部分の数字は「比」で出す
出典:『塾技100算数』p78
1 図形の平行移動:移動の作図の場合「1点ずつ」動かす
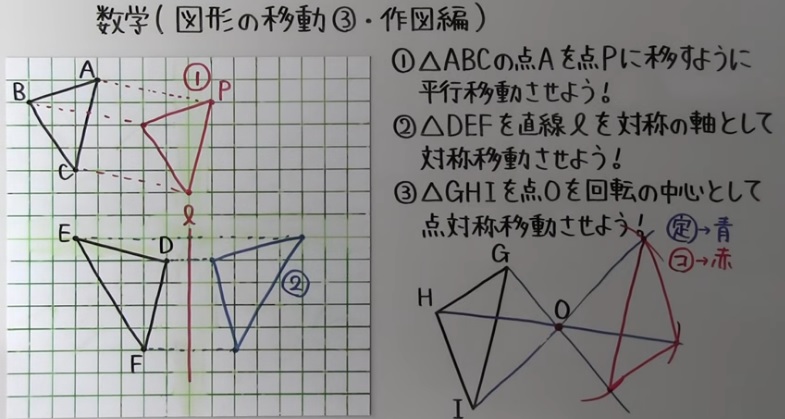
出典:https://www.youtube.com/watch?v=bSR0GazSMOQ
図形を平行に移動させて作図をする場合のポイントは、
「一点ずつ動かす」
という事です。
上記であれば、三角形を同時に動かそうとするとほぼ確実に混乱します。
AならA、BならB、CならCを一点ずつ正確に動かし、他の点を同じだけ
動かして最後に直線で結べばOKです。
「Aが右に5下に2」なら、当然「Bも右に5下に2」です。
ポイントは、
「一点ずつ動かす」
という事です。
2 両方動いている時は「差」を使う(片方止める):1秒ごとに何cm動くか
出典:https://www.youtube.com/watch?v=Keyd-deQiBo
図形の平行移動で中学受験の算数の問題になるのはどちらかというと
こちらの「動いている図形」が作る面積や形や長さの方です。慣れれば
いけるでしょう。
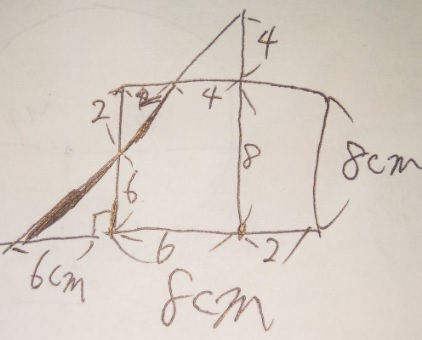
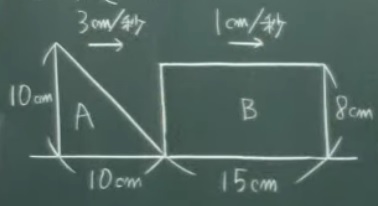
例題)1)下記の図形で2秒後の重なり部分の面積は何cm²ですか?
2)6秒後の重なり部分の面積は何cm²ですか?

出典:https://www.youtube.com/watch?v=Keyd-deQiBo
当然ですが、「図を正確に書く」のが基本です。
両方動いている時は「差」を使う(片方止める):1秒ごとに何cm動くか
両方が動いている場合、どちらかを止めて「差」で考えます。基本的には
追いかける方が速いので、追いつかれる方を止めます。
上記であれば「差」は3cm/秒と1cm/秒ですから、1秒ごとに2cm縮まります。
また、
重なり部分の数字は「比」で出す
ですので、上記の三角形は直角二等辺三角形なので、底辺の重なりと高さの重なり
の比は同じになります(四角形が高さ8cmなので高さの最大値は8cmですが)。
図を書いてみましたか?

(1)8cm²
(2)48cm²
3ぶつかる形の場合は両者の「和」の速さで動く(「出会い算」)
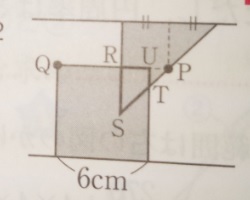
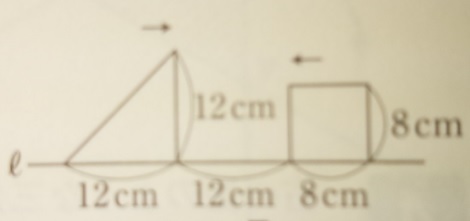
例題)下記の図は直角二等辺三角形と正方形です。どちらも毎秒1cmの
速さで直線lの上を矢印の方向に進むとき、9秒後の重なった部分の面積
は何cm²ですか?
1 移動の作図の場合「1点ずつ」動かす
2 両方動いている時は「差」を使う(片方止める):1秒ごとに何cm動くか
(追いかける形の場合「追いつき算」)
3ぶつかる形の場合は両者の「和」の速さで動く(「出会い算」)
(ぶつかる形でも「片方止めて」考えるのは有効です)
4 重なり部分の数字は「比」で出す

図を書いてみましょう。
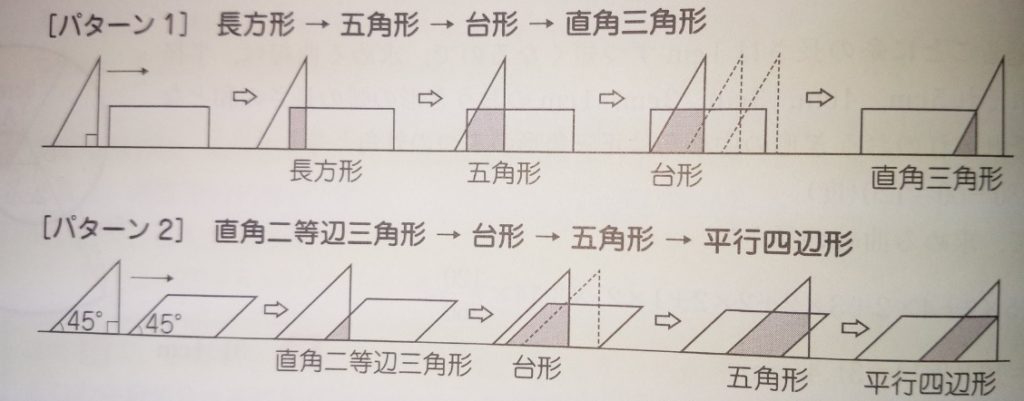
よく出る三角形と四角形の重なりの部分の変化

出典:『塾技100算数』p78
直角と45°があるので「二等辺三角形」が頻出します。
正確に図を書いて、どこの角度がどこと同じかといった
事をきちんと書き込みましょう。
問題)日本大学第二中学
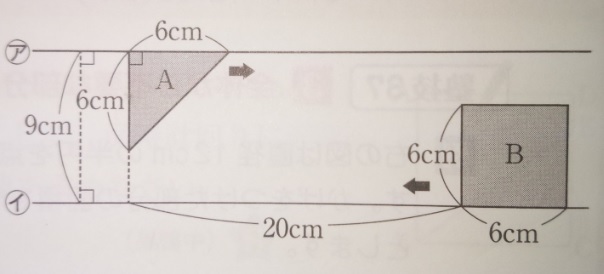
Aは二等辺三角形、Bは正方形です。
Aは毎秒1cmで矢印の方に、Bは毎秒3cmで矢印の方に動きます。
同時に動き始めた場合以下の問いに答えてください。
(1)AとBが重なり始めるのは動き始めてから何秒後ですか?
(2)動き始めてから6秒後の重なり部分の面積は何cm²ですか?
まとめ
1 移動の作図の場合「1点ずつ」動かす
2 両方動いている時は「差」を使う(片方止める):1秒ごとに何cm動くか
(追いかける形の場合「追いつき算」)
3ぶつかる形の場合は両者の「和」の速さで動く(「出会い算」)
(ぶつかる形でも「片方止めて」考えるのは有効です)
4 重なり部分の数字は「比」で出す

出典:『塾技100算数』p78
上記の問題集などでたくさん飽きるほど問題を解きましょう。
おうぎ形の面積の求め方2つと葉っぱ(レンズ)形の面積の求め方3つ!
ひもを巻きつけた図形・円の長さは「直線」と「曲線」に分ける!
図形の周りをひもが回っていく場合の考え方(つながれた犬が動ける面積)