図形の回転移動の書き方
1 時計をイメージする(移動した跡は【弧やおうぎ形】になります)
2 一点ずつ動かす
3 1点を選び、回転の中心からの距離を測る
4 3の点と回転の中心との角度を測り、回転させるべき角度に3で測った距離に印をつける
5 他の点も同じように印をつける
6 つけた印を結ぶ:回転移動した図形になる
いくつか「図形の回転移動の実例」を見てください。
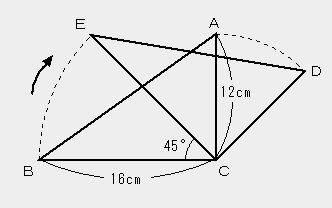
三角形ABCを頂点Cを中心にして45度回転させて、三角形DECを作ったものです。
問題)頂点Bが動いた跡の線(点線)の長さは何cmですか?
半径16cm、中心角45度のおうぎ形の弧の長さという事が
分かればできますよね?
(16+16)×3.14×45/360
=32×3.14×1/8
=4×3.14
=12.56
答え)12.56cm
問題)(同じ図の)辺ACが動いたあとの図形の面積何cm²ですか。

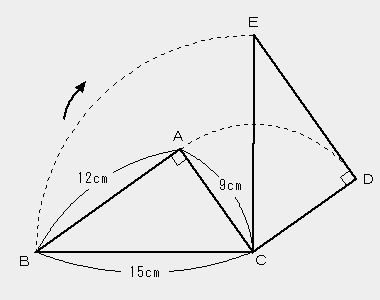
直角三角形ABCを頂点Cを中心にして90度回転させたものです。
BCに対応するのはECです。90度回転させています。
ですのでBCEの角度は直角(90度)になります。
問題)頂点Bが動いた跡の線(点線)の長さは何cmですか?
回転移動後の面積を求めるポイント
【移動後の面積を求めるには「等積移動」を利用すると良い】
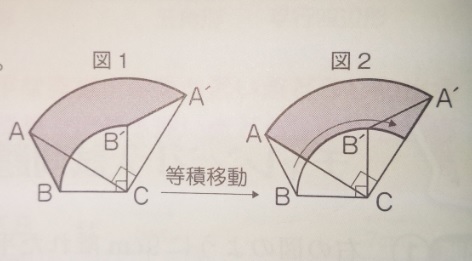
出典:『塾技100算数』p80
上記の図は三角形ABCがCを中心に90度回転しています。
AC=5cm、BC=3cmで、円周率は3.14。
仮に「辺ABが通過した部分の面積を求めなさい」という
問題があったとすると、図1の色部分を求める必要があり
ます。

そうすると、求める部分がきれいなおおぎ形にならず、計算がしづらい
ですが、上記の図の用に三角形部分を「等積移動」させることで
解きやすくなります。
(5×5×3.14×90/360)-(3×3×3.14×90/360)
=(25×3.14×1/4)ー(9×3.14×1/4)
=(25/4-9/4)×3.14
=16/4×3.14
=4×3.14
=12.56
答え)12.56cm²
*必ず「分配算」(分配法則)を使って計算しましょう
回転図形の問題パターン1:全体から不要部分を引く
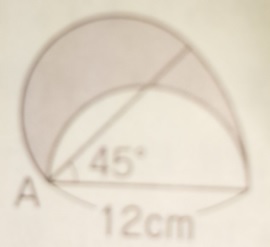
斜線部分の面積を求めなさい系の問題です。
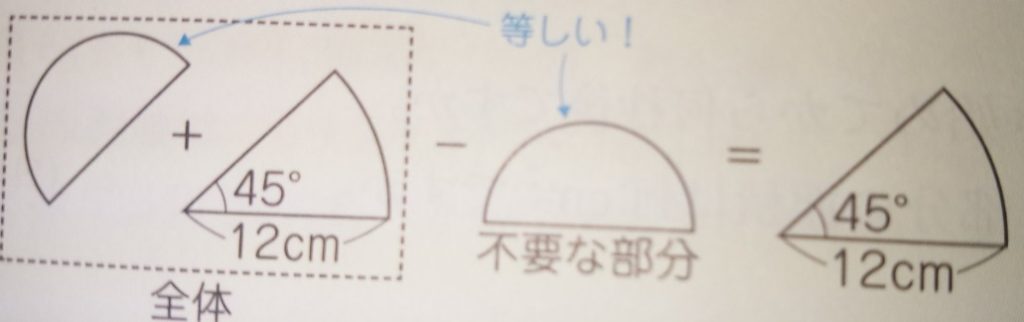
出典:『塾技100算数』p80
上記の形は意外といけるのではないでしょうか?
補助線を引く系問題(桐光学園中学)
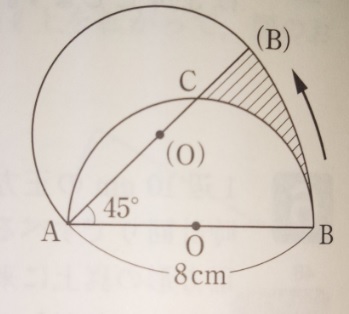
(1)点Bがえがく曲線の長さは何cmですか?
(2)弧ACの長さを求めなさい
(3)斜線部分の面積を求めなさい
(1)は半径8cm、中心角45度のおうぎ形の弧の長さです。
(8+8)×3.14×45/360=16×3.14×1/8=2×3.14=6.28
答え)6.28cm
(2)は補助線が必要です。CとOを直線で結ぶと、ACOの二等辺
三角形になります(円の半径なので距離は同じ4cm)
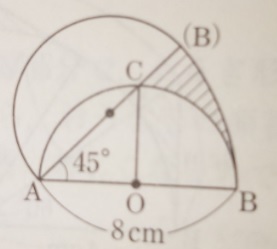
ですので半径4cmで中心角90度のおうぎ形の弧の長さが
弧ACです。
(4+4)×3.14×90/360=8×3.14×1/4=2×3.14=6.28
答え)6.28cm
(3)のような図で斜線部分を求めなさいという問題も典型パターンの一つです。
【全体から不要部分を引く】では微妙に解けませんね?
その場合、図形問題の王道ですが、どこかに補助線を引けないか
考えましょう。

①中心角45度で半径8cmのおおぎ形
②中心角90度で半径4cmのおおぎ形
③底辺4cm、高さ4cmの三角形
①-(②+③)=斜線部分の面積ですね?
(8×8×3.14×45/360)-(4×4×3.14×90/360+8)
=(64×3.14×1/8)-(16×3.14×1/4+8)
=(8×3.14)ー(4×3.14+8)
=25.12-20.56
=4.56
答え)4.56cm²
まとめ
図形の回転移動は、最初は難しいかもしれませんが、下記のポイントを
おさえてたくさんの問題を正確に解く事でできるようになるでしょう。
ぐあむばってください。
ポイント
時計をイメージする(移動した跡は【弧やおうぎ形】になります)
一点ずつ動かす
【移動後の面積を求めるには「等積移動」を利用すると良い】
全体から不要部分を引く
補助線を引く
おうぎ形の面積の求め方2つと葉っぱ(レンズ)形の面積の求め方3つ!