回転する図形2:円の回転数と多角形の周りをまわる際のポイント!
この記事では、
【円が「円やおうぎ形や三角形のまわり(外側)を回転する問題】
についてまとめています。
文系の人間の負け惜しみとして「え、え、え、え。それ何の意味が・・・」
と思いますが、試験を受けるのならば出題されるものはできるようにしな
ければなりませんので・・・。
なお「円が多角形の内側を回る」系の問題は下記の記事をどうぞ。
円が円の周りを回転する時のポイント
円が円の周りを転がる時は以下のようになります。
1)円の回転数=中心の移動距離(回転する円周)÷〔回転する円(小円〕の)円周
2)円の中心は弧を描いて回転します
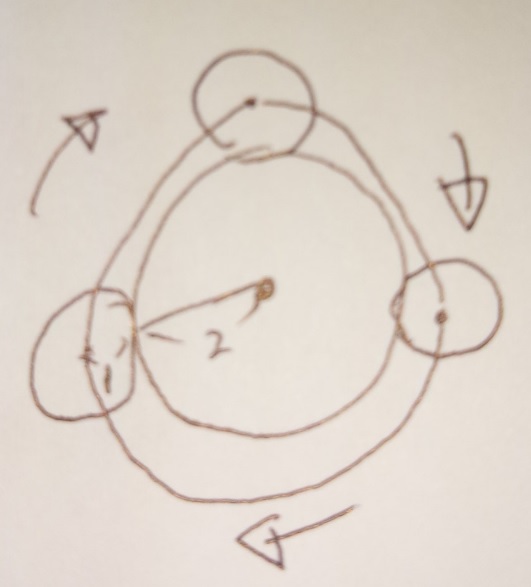
問題)上記の図で、半径1cmの円が半径2cmの円のまわりをすべらない
ように転がり1周します。この時、半径1cmの円は何回転しますか?
円周率は3.14です。
1)円の回転数=中心の移動距離(回転する円周)÷〔回転する円(小円〕の)円周
上記の図で言うと、小さい円の回転数は、
中心の移動距離(回転する円周)÷〔回転する円(小円〕の)円周
「中心の移動距離」は、
半径2cm+半径1cm=半径3cmで円を描きますので、その円周です。
(3+3)×3.14
〔回転する円(小円〕の)円周は
(1+1)×3.14
円の回転数=中心の移動距離(回転する円周)÷〔回転する円(小円〕の)円周
なので、
((3+3)×3.14)÷((1+1)×3.14)=6÷2=3
答え〕3回転
2)円の中心は弧を描きます
図の通りです。

円が多角形の周り(外側)を転がる時のポイント
出典:『塾技100算数』p84
円が多角形の周りを回転する時のポイント!
1)角を曲がる時は(円の中心は)おうぎ形の弧を描く
2)面積は【幅が一定の図形の面積=幅×中心線の長さ】を利用する

出典:『塾技100算数』p84
1)角を曲がる時は(円の中心は)おうぎ形の弧を描く
上記の図で分かるように、角は半径が円の直径と同じおうぎ形になります。
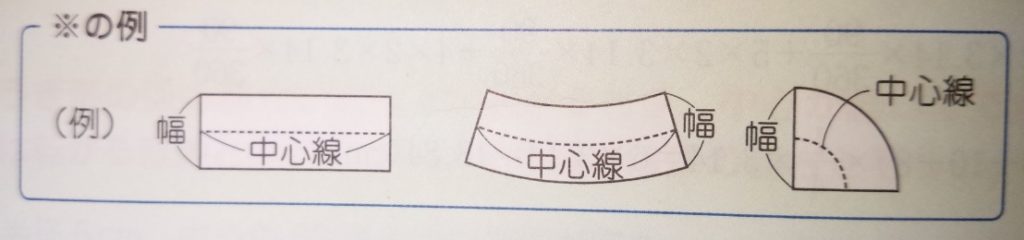
2)(直線部分は)【幅が一定の図形の面積=幅×中心線の長さ】を利用する
「中心線」は正方形や長方形の場合分かりやすいです。おうぎ形等もあります(下記参照)
出典:『塾技100算数』p84
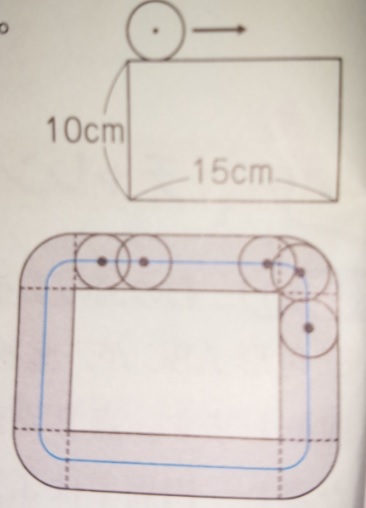
問題)下記の図の円は半径2cmです。長方形の外側を1周します。
(1)円の中心が描く線の長さは何cmですか?
(2)円が通った後にできる図形の面積は何cm²ですか?

*本来は上の図だけになりますが最初なので下の図も載せます・・・
(1)直線部分が、15×2と10×2で50cm、角のおうぎ形部分の
中心線は、半径2cmの円の所(青い線)が弧になりますので、
半径2cmの円の弧が90度×4つで円周分ですね。
(2+2)×3.14=12.56cm
50+12.56=62.56
答え)62.56cm
(2)【幅が一定の図形の面積=幅×中心線の長さ】
を利用すると、上記の図は幅が一定(4cm)なので
4×62.56=250.24
答え)250.24cm²
ただし、すぐにそれが浮かばない場合は普通に計算しましょう。
直線部分の面積は、縦が10×(円の直径)4=40が二つで80cm²
横の部分が15×(円の直径)4=60が二つで120cm²
直線部分は200cm²
角のおうぎ形は、半径4cm、中心角90度のおうぎ形が4箇所なので、
半径4cmの円の面積となる。
4×4×3.14=50.24
200+50.24=250.24
答え)250.24cm²
まとめ
円が円の周りを転がる時は以下のようになります。
1)円の回転数=中心の移動距離(回転する円周)÷〔回転する円(小円〕の)円周
2)円の中心は弧を描いて回転します

円が多角形の周りを回転する時のポイント!
1)角を曲がる時は(円の中心は)おうぎ形の弧を描く
2)面積は【幅が一定の図形の面積=幅×中心線の長さ】を利用する

出典:『塾技100算数』p84
回転する図形2:円の回転数と多角形の周りをまわる際のポイント!