(関連記事)
連比の問題と解き方のテクニック3つ!youtube音声動画付き
「線分図」
和も差も変化する倍数算は「線分図」で解く!どちらか一方の比率を最小公倍数で揃える!
やりとりの前後で、比率が変化する時の数字を求める問題を倍数算と言います。
倍数算には、
・和が一定
・差が一定
・和も差も変化する
問題があります。
「和が一定」「差が一定」の倍数算については、
にまとめてあります。
この記事では、
【和も差も変化する倍数算】
について学びましょう。
●【和も差も変化する倍数算は線分図を使う】
●「前後」の比率を考える(○と□のようにきちんと分ける)
●どちらか一方の比率を最小公倍数で揃えて、残りの比率を用いて数量を決める
先に言ってしまいますが、解法は以下です。
1)線分図を正確に書く:前後の比率をきちんと分ける
2)どちらかの比率を最小公倍数で揃える
3)もう一方の比率の差から割合が出せる
揃えることで「割合」が一つにできるという事ですね。
和も差も変化する倍数算は「線分図」で解く!
「和が一定」「差が一定」の倍数算については、
倍数算の問題は【連比】か【線分図】を使って解く
でしたが、
和も差も変化する倍数算は「線分図」で解く事を基本としましょう。
●【和も差も変化する倍数算は線分図を使う】
●「前後」の比率を考える
●どちらか一方の比率を最小公倍数で揃えて、残りの比率を用いて数量を決める
問題)だろう君とびばりさんの所持金の比は1:3です。だろうくんは誰かから
から50円もらい(びばりさんではありません)、びばりさんは100円使ったので、
その後の2人の所持金の比率は2:1になりました。
だろうくんの最初の所持金は?
和も差も変化していますね?
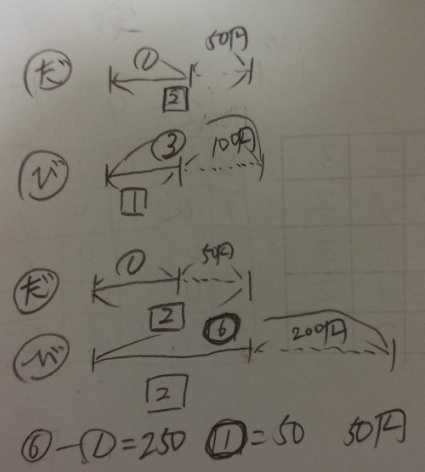
まずは「線分図」を書きましょう。
①と③の方が「前」の比率です。
□で囲っている方が「後」の比率です。
ポイントは
●どちらかの比率を最小公倍数で揃える●
後の比率を「2」で揃えます。
連比と同じなので、2倍したら、同じ組の所はすべて2倍ですから、
100円→200円、割合③→⑥です。
そうすると、割合⑥ー割合①=250円だと分かりますね?
割合⑤=250円なので割合①=50円
だろう君の最初の所持金は割合①ですから、
答え50円
問題)だろう君とびばりさんの所持金の比は、はじめ3:2でしたが、だろう君は
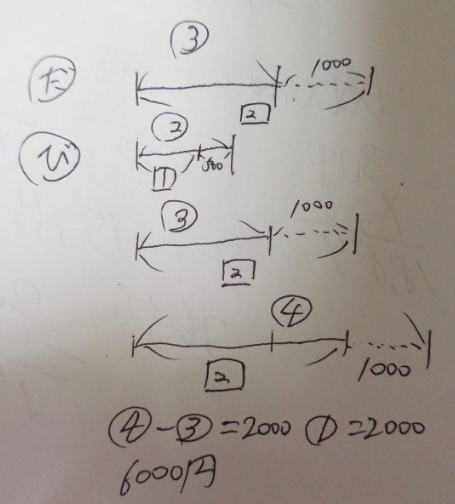
1000円もらい(びばりさんからではありません)、びばりさんは500円使ったので、
その比が2:1になりました。はじめにだろう君はいくら持っていましたか?
線分図を書いて解いてみましょう。
問題)清原中学校と桑田中学校の受験者数の比率は4:5で、合格者数は、
清原が120人、桑田が180人でした。不合格者数の比率は5:6でした。
清原中学校の受験者数は何人ですか?
考え方は同じです。
●線分図を正確に書く
●比率を前後できちんと分ける
●どちらかの比率を最小公倍数で揃える●
(揃えた方は他の数字も同じ倍数かけるのを忘れないように)
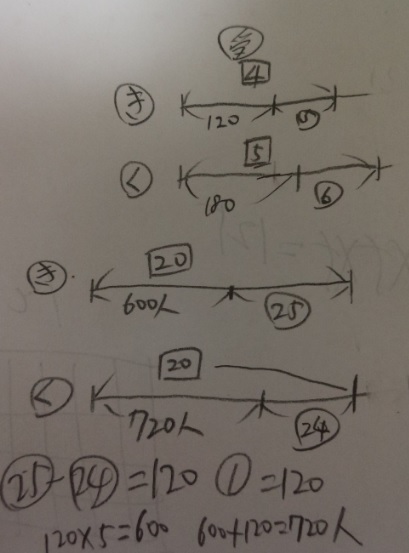
□が受験者数の割合です。○が不合格者数の割合です。
このままでは揃っていないので割合が出せません。
受験者数の割合「4」「5」の最小公倍数「20」で揃えます。
揃えているので総数は同じになります。
という事は不合格者数の割合①が120だと分かりますね?
清原中学の受験者数は、
120人の合格者+割合⑤(120×5)です
答え)720人
倍数算の中学入試問題等
問題)慶應中等部
初めに兄と弟が持っている鉛筆の本数の比は7:5でしたが、兄は友達から
鉛筆12本をもらい、弟は友達に鉛筆を4本あげたので、兄と弟の鉛筆の
本数の比は12:7になりました。初めに兄が持っていた鉛筆は□本です。
考え方は同じです。
●線分図を正確に書く
●比率を前後できちんと分ける
●どちらかの比率を最小公倍数で揃える●
(揃えた方は他の数字も同じ倍数かけるのを忘れないように)

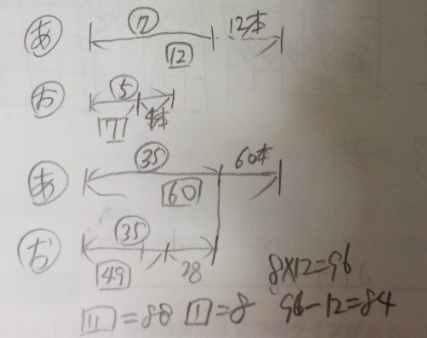
●上2本が問題文を線分図にしたものです
●最初の割合⑦と⑤を最小公倍数の35で揃えます
●「後」の割合の差「11」が88本という事が分かります
●割合①=8本です(あわてて8×7+12=68本!としないように)
●兄の最初の本数は、割合⑫から12本を引いた数です
●8×12-12=84
答え)84
まとめ
●【和も差も変化する倍数算は線分図を使う】
●「前後」の比率を考える(○と□のようにきちんと分ける)
●どちらか一方の比率を最小公倍数で揃えて、残りの比率を用いて数量を決める
●どちらかの比率を最小公倍数で揃える●
これがポイントになりますが、
揃えた方は他の数字も同じ倍数かけるのを忘れないように
しましょう。「連比」のテクニックと同じですね。
(関連記事)
連比の問題と解き方のテクニック3つ!youtube音声動画付き
「線分図」
和も差も変化する倍数算は「線分図」で解く!どちらか一方の比率を最小公倍数で揃える!