相当算を解くコツ5つはこれ!「残りの1/?を使って」系は、「（全体－初日）×二日目以降に使った割合」―「中学受験＋塾なし」の勉強法!

割合のテクニック（簡単に考える＋小数に直して「倍」＋「１」を正確に）

平均・比は面積図を書く（出っ張り＝凹み）

  

相当算とは？

相当算とは、

●分数で表す割合の文章題●

と考えておきましょう。

 

相当算を解くコツ5つ

 

基本問題はこれですべて解けます。

１と２は多くの人ができますが、

３　もとにする量＝割合にあたる量÷割合

5　全体（元にする・基準となる）が同じ割合同士なら、直接比べる事ができる

あたりから差がつきます。

また、相当算の典型的なパターンが、

4 　「残りの1/?を使って」系は、「（全体－初日）×二日目以降に使った割合」

です。初日に「全体の1/3を読んで、二日目に残りの1/3を読んで～～」といった

やつですね。初日の残りは全体の2/3ですから、2/3×1/3＝2/9で、二日目に

読んだ全体の中での割合が出せます（2/９）。

また、基本的な問題であっても、上記のコツをきちんと使っておいたほうが

難問になったときに慣れていて解きやすいです。とくに、

もとにする量＝割合にあたる量÷割合

は非常によくつかいます。

 

例題）

コップのジュースを全体の7/12を飲んだら残りは100mでした。

はじめにジュースは何mlありましたか？

考え方）

「割合に当たる量（100ｍｌ）」と「割合5/12（12/12-12/7）」

が分かっているので、

●もとにする量□＝割合にあたる量（100）÷割合（5/12）●

が使えますね？最初は線分図を書いた方が良いでしょう（慣れてきたら

このレベルの問題は筆算のみでも良いかと思います）。

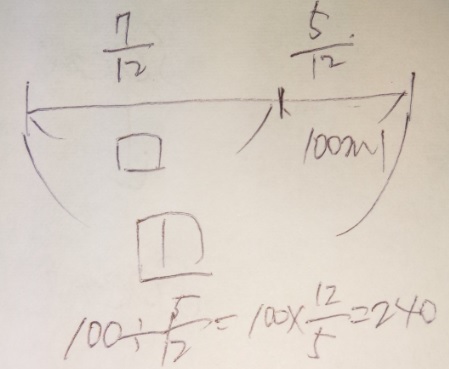
100÷5/12=240

答え）240ml

こういう素直な問題だけなら良いのですが・・・、現実（中学受験の算数）

はもっと難しいです。ですが、基本は同じなので、まずは基本をしっかりと

覚えましょう。

例題）

びばりさんは夏目漱石の『草枕』を読みました。最初の日に全体のページ数の

1/5を読みました。2日目に残りの1/8を読み、その後5日目までは、2日目と同じ

ページ数で読みました。5日目に読み終えたとき、残りは164ページでした。

びばりさんの読んだ『草枕』は全部で何ページありますか。

考え方）

こういう問題になると線分図を書かないと話しになりませんね。

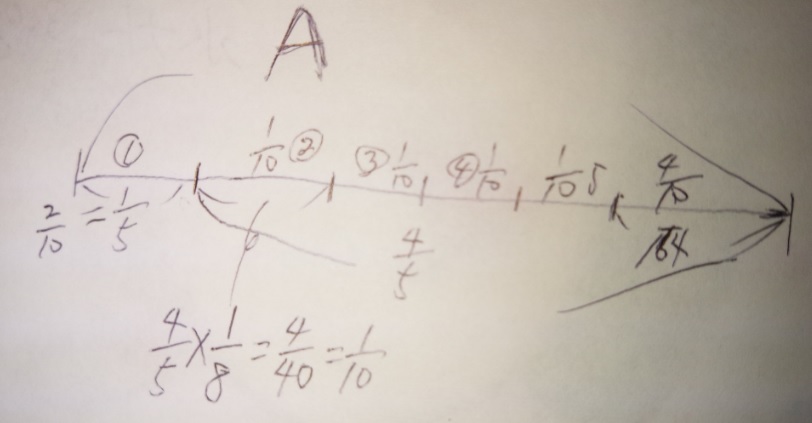
み、みづらいですか・・・。これくらいの方がリアルで良い？

１：全体をAとして線分図を書いていきます

２：初日①が全体の1/5

３：二日目から5日目までの4日間が残りの1/8ずつ

４：二日目の残りは（初日が1/5なので）4/5＊たぶんここが分かればいける

　　ということは、4/5の1/8が2日目~5日目に読んだ全体の中での量

　　ということは4/5×1/8=1/10が2日目~5日目に読んだ全体の中での量

５：初日1/5、2日~5日目が1/10という事は、初日~5日目で全体の6/10

６：残りは全体の4/10（2/5）

７：全体の2/5にあたるのが164p

8：もとにする量＝割合にあたる量÷割合

9：164÷2/5=81×5＝410

答え）410p

 

相当算の中学入試問題等

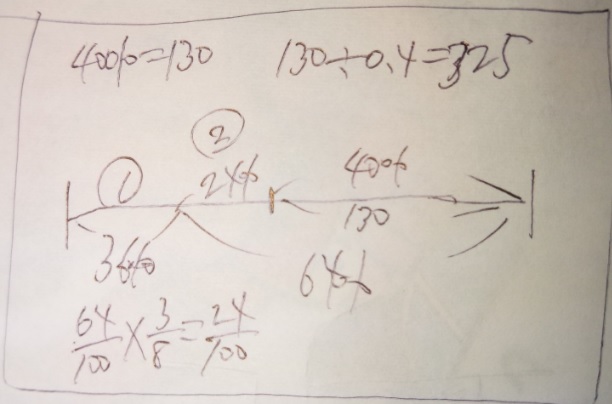
問題）桐朋中学

ある商品を何個か仕入れました。初日は全体の36%が売れ、2日目は残りの

3/8が売れたので、商品は130個残りました。仕入れた商品は何個ですか？

正確な線分図が書けるかどうかです。

分数で計算しても答えにたどり着いていればもちろん問題ありません。

      

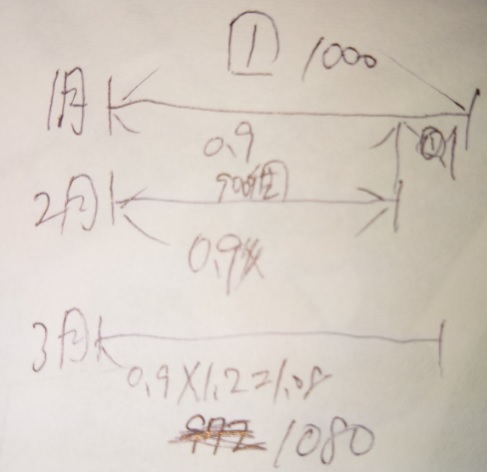
問題）吉祥女子中学

ある商品の2月の売上個数が1月の売上個数よりも10%減りましたが、

3月の売上個数は、2月の売上個数よりも20%増えました。2月の売上

個数が900個のとき、3月の売上個数は1月の売上個数より何個多いか

答えなさい。

ある種のパターン化された問題と言えます。冷静に線分図を書いて

みましょう（問題文を正確に線分図にするのが解くための80%くらいでしょうか）。

 

下記の問題集（相当算は『算数文章題』か『塾技』が良いです）でガンガン

問題を解きましょう。量をこなすと質に転化します。量をこなさないと

算数的に高品質な頭にはなりません。

    

割合のテクニック（簡単に考える＋小数に直して「倍」＋「１」を正確に）

平均・比は面積図を書く（出っ張り＝凹み）