物の熱量・温まり方(熱とは?熱の移動・温度の違う2つの水・カロリー)
そもそも「熱」とは?
「熱」とは、物の温度を上げるエネルギーの事です。
物の温度は状態によって「冷たい→温かい→熱い」と変化しますよね?
その際に温度を上げるエネルギーになるのが「熱」です。
温度は℃(セ氏)で表す
温度の表し方は3つあります(セ氏、華氏、ケルビン)。
日本では「セ氏(℃)」が使われます(アメリカでは華氏です)。
セ氏(℃)の基本
水の融点(とける温度)がセ氏0(0℃)。沸点が100℃。その間を
100等分して1度を決めています。
「熱」は移動する
熱は温度が高いものから低いものへと移動します。
最後は、両方の温度が同じになります。
セ氏80℃の水と20℃の水を混ぜると以下の図のようになります。
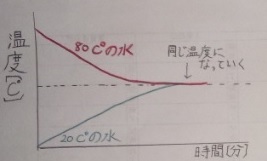
最終的には同じ温度になりますが、時間はそれぞれの量によって
変わります。
水の量と温度変化の比は逆比になります。
→水の量が増えると温度は上がりづらいです
→温度の変化は水の量に反比例します(水の量が1:2なら温度変化は2:1)
「温度の違う2つの水が触れる」系問題の解き方
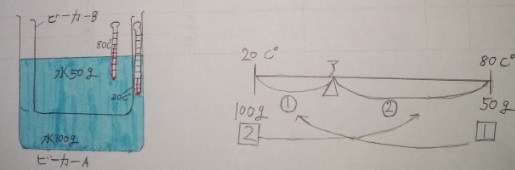
例題)上の図には、20℃の水が100g入っているビーカーAの
中に80℃の水が50g入っているビーカーBを入れてしばらく
置いたところ、2つのビーカーの温度が同じになりました。
何度になりましたか?ただし、熱は空気中には逃げないものと
します。

「温度の違う2つの水が触れる」系問題の解き方は
1)水の比率を出す
2)(水の比率の逆比が)温度変化の比率
3)天秤図(線分図・面積図)を描く
これが基本です。
上の問題ですと、
1)水の比率を出す→100(A):50(B)→2(A):1(B)
2)(水の比率の逆比が)温度変化の比率→1(A):2(B)
3)天秤(てんびん)図(線分図・面積図)を描く(下図の右側が「天秤図」)

算数の「線分図」と同じ考え方です。
80℃ー20℃=60℃です。60℃を割合③で分ければ、①は20です。
60÷3=20
ということは「ア」は20+20=40℃
答え)40℃
例題)60℃の水100mlと30℃の水100mlを混ぜてできる200mlの水は何度に
なりますか?もっとも近いものを選び、記号で答えなさい。(お茶の水女子大付属中学)
ア約40℃ イ約45℃ ウ約50℃ エ約55℃
「熱量」=カロリー
「熱」とは、物の温度を上げるエネルギーの事でしたが、その「熱」を
数量的に表したものを「熱量」といい、単位はカロリーです。
カロリーについての基本
1)1gの水の温度を1℃上げるのに必要な熱量が1カロリー
2)1gの物の温度を1℃上げるのに必要なカロリーは物によって異なる
3)上記の1)から以下の式が成り立つ
水の重さg×変化した温度℃=熱量(カロリー)
ex)
100gの水を10℃あげるために必要なカロリーは100×10=1000カロリー
1gの水を5℃あげるために必要なカロリーは1×5=5カロリー
12歳くらいですと、約2000000(約200万)カロリーを消費すると
言われています。2000000g(2000kg)の水を1℃上げる熱量ですね。
まとめ
「熱」とは、物の温度を上げるエネルギーの事
熱は温度が高いものから低いものへと移動:最後は、両方の温度が同じ
水の量と温度変化の比は逆比
(温度の変化は水の量に反比例(水の量が1:2なら温度変化は2:1))
「温度の違う2つの水が触れる」系問題の解き方は
1)水の比率を出す
2)(水の比率の逆比が)温度変化の比率
3)天秤図(線分図・面積図)を描く
●カロリー●
1)1gの水の温度を1℃上がるのに必要な熱量が1カロリー
2)1gの物の温度を1℃上げるのに必要なカロリーは物によって異なる
物の熱量・温まり方(熱とは?熱の移動・温度の違う2つの水・カロリー)