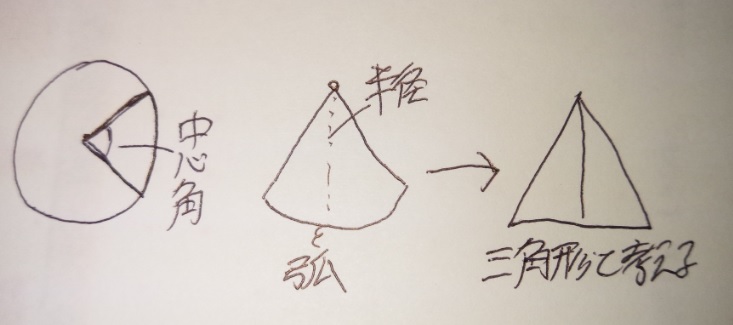
おうぎ形の面積の求め方2つと葉っぱ(レンズ)形の面積の求め方3つ!
おうぎ形の面積の公式2つ
1 半径×半径×3.14×中心角/360
2 弧の長さ×半径÷2

おうぎ形の面積を求める二つの公式のうち、
【1 半径×半径×3.14(円周率)×中心角/360】
は円の面積を求める公式に「×中心角/360」という「おうぎ」
の部分を指定して求める感じなので分かりやすいのでは?
【2 弧の長さ×半径÷2】
こちらに関しては、覚えてしまって良いと思います。
いずれにせよ、この二つの公式のどちらかを、何らかの形で
使って面積を求めていく問題が多くなります。
ハッパ形(レンズ形)のおうぎ形面積の求め方3つ!

(画像出典:「中学受験 算数の基本問題」)
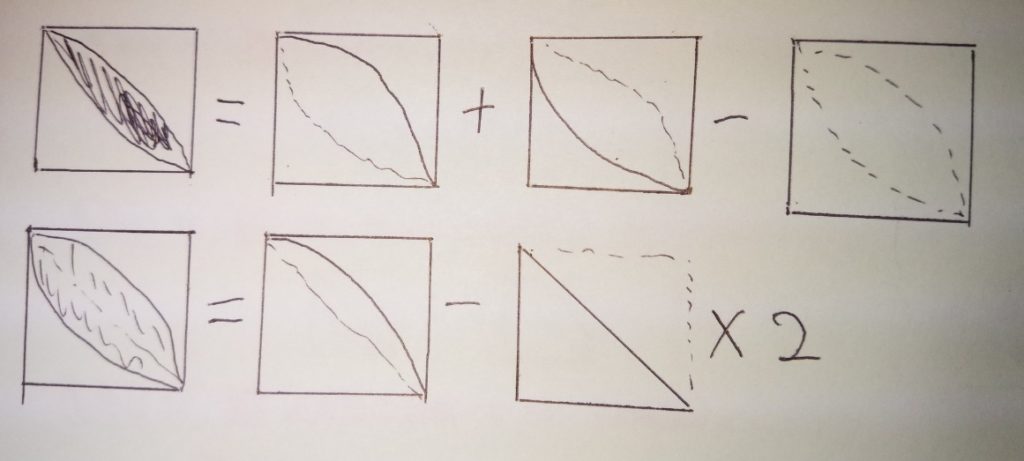
ハッパ形(レンズ形)のおうぎ形の面積の求め方
1 90度のおうぎ形2個-正方形
2 (90度のおうぎ形-半径×半径÷2(三角形))×2
3 正方形の面積×0.57 (円周率は3.14)

1 90度のおうぎ形2個-正方形(上の図)
上下からおうぎ形を見て、2個分の面積を出し、正方形の面積を引くと
真ん中のハッパ(レンズ)部分の面積が残ります。図を見ると分かりますかね?

2 (90度のおうぎ形-半径×半径÷2(三角形))×2(下の図)
90度のおうぎ形の面積を出し、そこから(半径×半径の二等辺)三角形
の面積を引くと、葉っぱ(レンズ)の半分が出ます。それを2倍にしてます。
これは図を見ると分かるのでは?

3 正方形の面積×0.57 (円周率は3.14)
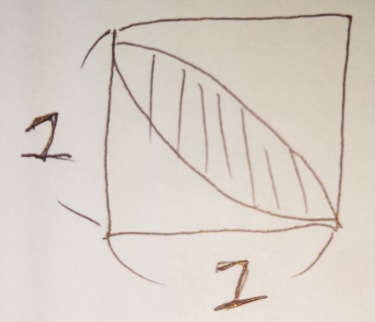
3 正方形の面積×0.57 (円周率は3.14)
が成り立つ理由を1辺1cmの正方形の中にあるおうぎ形で証明してみます。
1 90度のおうぎ形2個-正方形
この公式を使って式を作ると、
1×1×3.14×90/360=3.14×0.25=0.785
これがおうぎ形の面積です。
1 90度のおうぎ形2個-正方形
ですので、0.785×2-(1×1)=1.57-1=0.57
答え)0.57
ですね?
葉っぱ(レンズ形)のおうぎ形の面積は
正方形の面積×0.57 (円周率は3.14)
でも出せると「0.57」を覚えてしまってもいいです。
等積移動:図形を移動させて考える+おうぎ形・三角形・四角形を作る
算数の図形では
●補助線を引く●
というのは基本で、絶対に必要です。おうぎ形系の問題では、
「補助線を引く」に加えて、
●同じ面積の所を移動させる●(等積移動)
というものを覚えてください。
理屈としては、等積移動は、そのままでは面積を求めづらい問題を解く
ために、図形の一部を移動させ、おうぎ形や三角形、四角形を作って
面積を求めます。
文字で書かれても???ですよね?図を見て理解しましょう。
ある程度パターン化されているので、何度もやっていると覚えてしまえ
ます。
また、中学受験の算数入試問題レベルになると、等積移動させないと、
あるいはパターンを知らないと(少なくとも時間内には)解けない問題
というのが基本になっていたりします・・・。世知辛い世の中ですね。
おうぎ形の面積(等積移動系)を求めよ問題のパターン
1 等積移動:同じ面積の所に移動させて計算しやすくする
2 葉っぱ4枚:小さい正方形4つに分ける(正方形の面積×0.57)
3 補助線+等積移動:補助線を引いて等積移動する
4 ヒポクラテスの三日月(直角二等辺三角形):三日月の面積=直角三角形の面積
5 1~4の組み合わせ(難関中学):上記をマスターしてさらに問題に慣れる
【1 等積移動:同じ面積の所に移動させて計算しやすくする】

出典:『塾技100算数』p72
上記の図でいうと、
1 左下のおうぎ形の面積を等積移動させ、右のおうぎ形を作る
2 大きいおうぎ形の面積を求める
3 「2」の面積から三角形の面積を引く
【2 葉っぱ4枚:小さい正方形4つに分ける(正方形の面積×0.57)】
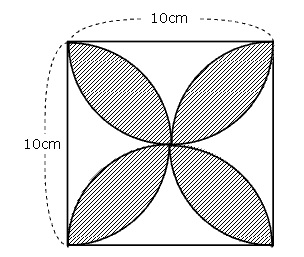
問題)斜線部分の面積は?
葉っぱ(レンズ)4枚形です。大きい正方形を小さい正方形(1辺5cm)
4つに分けて考えます。円周率3.14なら以下の公式が使えます。
正方形の面積×0.57 (円周率は3.14)
5×5×0.57=14.25(葉っぱ一枚の面積)
14.25×4=57
答え)57cm²
【3 補助線+等積移動:補助線を引いて等積移動する】

出典:『塾技100算数』p72
この問題はある意味では【補助線】+【等積移動】ですね。
たくさん問題を解くとこのパターンが多数出てきます。
【4 ヒポクラテスの三日月(直角二等辺三角形):三日月の面積=直角三角形の面積】
この「ヒポクラテスの三日月」の形はそのまま出てくる事もよくあります。
直角三角形であれば必ず
「(上の)三日月の面積=直角三角形の面積」
になります。
黄色部分の面積を求める場合、直角三角形の面積を求めるだけでもOKです。
圧倒的に時間が節約できます。
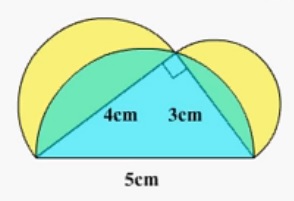
結論から書くと、黄色の三日月部分の面積は直角三角形の面積と
同じなので、3×4÷2=6 6cm²です。
「ヒポクラテスの三日月:三日月の面積=直角三角形の面積」を
知らない場合、以下のような解き方になります。証明ですね。

1 全ての面積を求める:三角形+直径4cmの半円+直径3cmの半円
2 「1」から直径5cmの半円の面積を引く
(3×4÷2)+(2×2×3.14÷2)+(1.5×1.5×3.14÷2)=
=6+6.28+3.5325
=15.8125 (全部の面積)
2.5×2.5×3.14÷2=9.8125
15.8125-9.8125=6 6cm²
面倒ですよね?
ここでもう一度式を見てみますと、
(3×4÷2)+(2×2×3.14÷2)+(1.5×1.5×3.14÷2)ー(2.5×2.5×3.14÷2)
はい!「3.14÷2を使って分配法則使えるんじゃね?」と思った方、ヒポクラテス
並の算数のセンスですね。
(3×4÷2)+(2×2×3.14÷2)+(1.5×1.5×3.14÷2)ー(2.5×2.5×3.14÷2)
=(3×4÷2)+(2×2+1.5×1.5ー2.5×2.5)×3.14÷2
=(3×4÷2)+(4+2.25-6.25)×3.14÷2
=(3×4÷2)+0×3.14÷2
=(3×4÷2)
分かりましたかね?
1 全ての面積を求める:三角形+直径4cmの半円+直径3cmの半円
2 「1」から直径5cmの半円の面積を引く
をしていくと、途中で「三角形だけの面積が答え」に必ずなります。
理由は「三平方の定理」です。
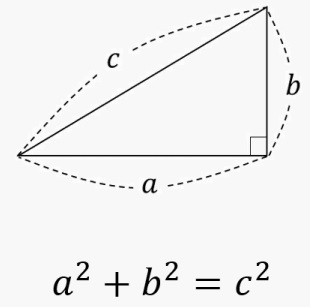
三平方の定理(ピタゴラスの定理)は中学受験では出ませんので、
詳細は知らなくても良いですが、直角三角形の3辺の長さの公式です。
=(3×4÷2)+(4+2.25-6.25)×3.14÷2
上記の問題では、上の部分ですね。必ず0になります。
ですので、直角三角形であれば、「ヒポクラテスの三日月」が
使えます。
「(上の)三日月の面積=直角三角形の面積」
になります。
黄色部分の面積を求める場合、直角三角形の面積を求めるだけでもOKです。
圧倒的に時間が節約できます。

円とおうぎ形の中学入試問題等

問題)上記の図の斜線の部分の面積を求めてください。
円周率は3.14とします。
この形は飽きるほど出てくるので、反射的に
正方形の面積×0.57 (円周率は3.14)
を使ってもよさそうです。
問題)斜線部の面積を求めてください。円周率は3.14です。
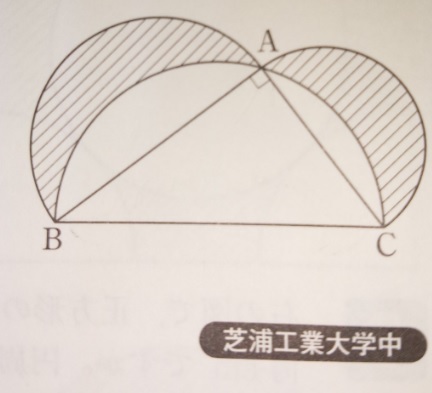
問題)芝浦工業大学中学校
下記の図の斜線部分の面積を求めなさい。円周率は3.14です。
AB8cm, BC10cm,CA6cmです。
上記に解説した「ヒポクラテスの三日月」をもう一度復習しておきましょう。
おうぎ形の面積の求め方2つと葉っぱ(レンズ)形の面積の求め方3つ!