回転する図形2:円の回転数と多角形の周りをまわる際のポイント!
円が多角形の外側を回る場合は、下記記事にまとめました。
回転する図形2:円の回転数と多角形の周りをまわる際のポイント!
この記事では、「円が図形の内側を転がる時のポイント」についてまとめました。
「おうぎ形のスキマ」が大事です!
円が図形の内側を転がる時のポイント
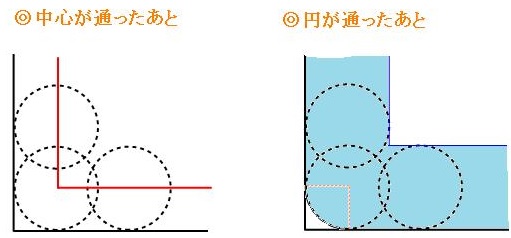
画像出典:https://jukensansuu.com/syuujou.html
【円が図形の内側を回る時のポイント】
1)中心線が描く線は直線のみ
2)円が通った面積は角におうぎ形の分スキマができる
(円の半径1辺とする正方形-中心角90度のおうぎ形)
3)内側だけれど外側のように回る場合はスキマができないので注意
4)長方形の内側を円が1周すると、円の直径2つ分短い長方形が中にできる

画像出典:https://jukensansuu.com/syuujou.html
1)中心線が描く線は直線のみ
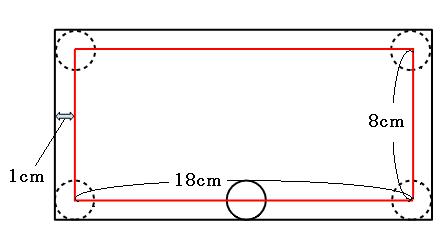
画像出典:https://jukensansuu.com/syuujou.html
ですから、中心線が描く線の長さは、18×2+8×2=52 52cmです。
2)円が通った面積は角におうぎ形の分スキマができる
スキマの面積は
(円の半径を1辺とする正方形-中心角90度のおうぎ形)
になります。
スキマが4箇所であれば、「スキマの面積×4」あるいは、
「円の直径を1辺とする正方形ー円の面積」ですね。

図を見れば分かりますが、「円の半径を1辺とする正方形」です。
3)内側だけれど外側のように回る場合はスキマができないので注意

右側はいわば、外側を回っているようなものですからね・・・。
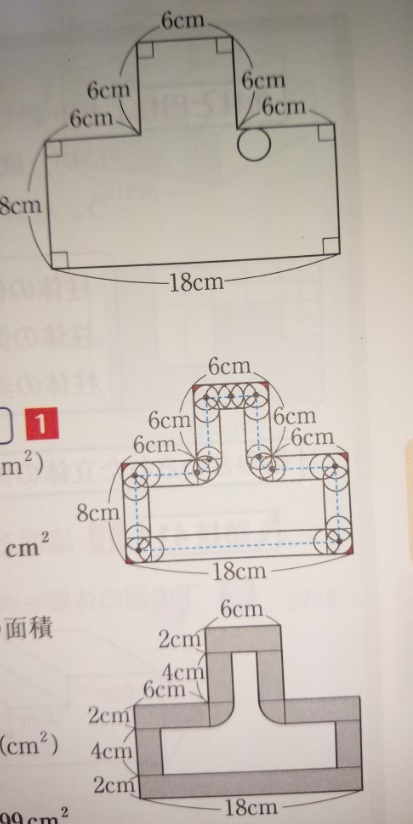
出典:『塾技100算数』p86-87
上記のような場合、内側だけど、外側を回っているようになる
真ん中のおうぎ形部分には内側にはスキマができません。
4)長方形の内側を円が1周すると、円の直径2つ分短い長方形が中にできる
これは図を見るのが一番分かりやすいでしょう。
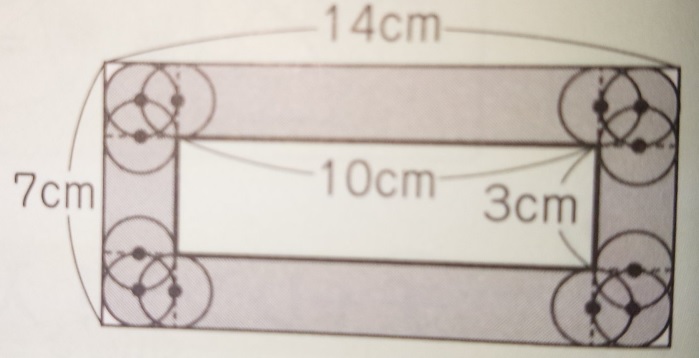
上下左右を円が通るので、「円の直径2つ分短い」長方形になります。
という事は、
円が通った面積を求める場合、
①長方形全体から通らない部分の面積を引く(スキマを忘れないように)
事で可能となります。もちろん、
②円が通る部分の面積から角のスキマを引く
でも良いです。
【円が図形の内側を回る時のポイント】
1)中心線が描く線は直線のみ
2)円が通った面積は角におうぎ形の分スキマができる
(円の半径1辺とする正方形-中心角90度のおうぎ形)
3)内側だけれど外側のように回る場合はスキマができないので注意
4)長方形の内側を円が1周すると、円の直径2つ分短い長方形が中にできる
問題)
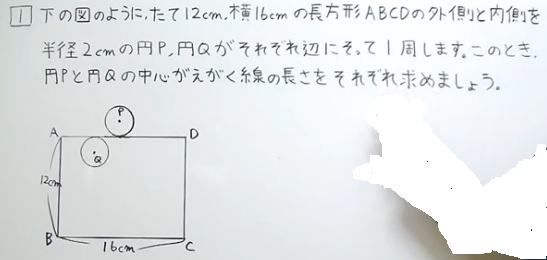
出典:YouTube
外側と内側の両方を知らないとできませんね。
外側統治がを別々に計算しますか。きちんと図を描いてみましょう。
「外側」
直線部分:16×2+12×2=56
おうぎ形部分(4箇所で円になる):半径2cmなので、2×2×3.14=12.56
56+12.56=68.56
答え)68.56cm
「内側」
内側は「描く線」は直線のみなので、
12×2+8×2=40
答え〕40cm
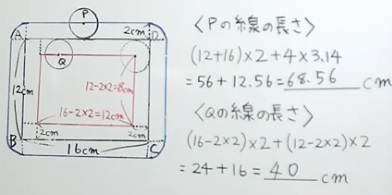
出典:YouTube
どうですか?できましたか?
計算を間違えていた場合は、きちんとやり直しましょう。
そもそも解き方が分からない場合、もう一度最初から読み直しましょう。
算数はルール・手続きに則って解けば必ず正解にたどりつきます!
(人生は「必ず正解にたどりつくルール」があるとは限りませんが、
算数はあります!そもそも「人生の正解」ってなんやねん!)
まとめ
【円が図形の内側を回る時のポイント】
1)中心線が描く線は直線のみ
2)円が通った面積は角におうぎ形の分スキマができる
(円の半径1辺とする正方形-中心角90度のおうぎ形)
3)内側だけれど外側のように回る場合はスキマができないので注意
4)長方形の内側を円が1周すると、円の直径2つ分短い長方形が中にできる
回転する図形2:円の回転数と多角形の周りをまわる際のポイント!
