
(関連記事)
食塩水問題(濃度算)は2つ分かれば解ける!ビーカーの図・面積図を描け!
逆比とは?
「逆比」?あ~あれでしょあれ、比率の数字を逆に
するやつでしょ?→正確にはちょっと違います。
(「2つの数の比」の場合のみ、結果的に逆比は比率を逆にしたものになります)
逆比とは「逆数」の比の事です。
【逆数とは、その数にかけると1になる数】
です。2なら1/2、3なら1/3、15なら1/15ですね?

上の図でも分かるように、
2:5→逆比→5:2というのはあくまでも「結果」であって、
【2:5→逆比→1/2:1/5→1/2×(2×5):1/5×(2×5)→5:2】
というのが「分かっている」理解の仕方です。
逆比とは「逆数」(かけたら「1」になる数字)の比
の事です。
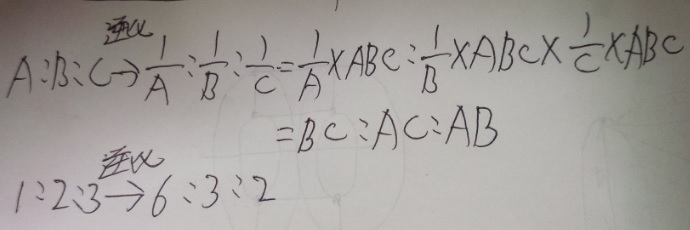

例えば、
「ある金額で、ジュースなら90本、サンドイッチなら36個、ケーキならば40個買える」
といった場合、それぞれ1個当たりの金額の比は個数の比の逆比になります。
簡単に考えると、1000円持っていて、ジュースなら10本(1本あたり100円)、サンドイッチ
なら5個(1個当たり200円)、ケーキなら2個(1個当たり500円)
買えるなら、それぞれ1個当たりの金額の比は個数の比の逆比になりますというのが分かりますよね?
個数 1個あたりの金額
10:5:2→逆比→1/10:1/5:1/2=1:2:5
慣れた場合(基本が完璧なら)2つの数字は、比率はひっくり返しても良いです。
基本が完璧ならです。
逆比は何に使うのか?
逆比は、中学受験の算数では結構使い勝手があります。
●面積、食塩水問題、速さと時間、仕事算etc
「速さと時間」などは、逆比を使うと圧倒的に速く解けます。
中学受験の算数は時間との勝負でもありますので、「速い」事は大事です。
慣れるという意味では、問題を見て、
「あ、これは「逆比」を使えって事ね」
となるくらいが理想です。逆に言うと、逆比を使わないと意味不明(略して
「イミフ~~~」)の問題がたくさんあります。
まあ、実際に問題にあたるのがいちばんいいでしょう。
逆比の中学受験問題等
問題)だろう君は時速3kmの速さで歩きます。びばりさんは時速4kmの
速さで歩きます。だろう君が4時間で着いた場所にびばりさんは何時間で着きますか?
これは暗算でもできますが、「速さと時間」の問題は、逆比を使うとやりやすいです。
速さ 時間
3:4→逆比→1/3:1/4→4:3
という事は、だろう君が4時間という事は、びばりさんは3時間ですね?
答え)3時間
問題)だろう君は時速2kmの速さで歩きます。びばりさんは時速3kmの
速さで歩きます。だろう君が6時間で着いた場所にびばりさんは何時間で着きますか?
速さ 時間
2:3→逆比→1/2:1/3→3:2
だろうくんの時間が6なら、びばりさんの時間は4ですね?
答え)4時間
問題)Aの3倍とBの4倍が等しい時、AとBの比はいくつですか?
A×3=B×4ですから、AとBの比は、3と4の逆比(かけて1になる)になりますね?
3:4→逆比→1/3:1/4→4:3
答え)4:3
問題)Aの2倍とBの3倍とCの4倍が等しい時、A:B:Cの比はいくつですか?
A×2=B×3=C×4ですので、2,3,4の逆比(×と1になる)がA:B:Cですね?
2:3:4→逆比→1/2:1/3:1/4→6:4:3
答え)6:4:3
数字が3つ以上の場合、「比率を逆にする」は通じませんよ。
逆比とは「逆数」の比の事です。
【逆数とは、その数にかけると1になる数】
を頭にきちんと入れましょう。
問題)だろう君はAからBまで20分かかります。びばりさんはAから
Bまで30分かかります。AとBの距離が500mの時、だろうくんがAから、
びばりさんがBから出発すると、Aから何m離れた地点で二人は出会いますか?
時間と距離は逆比になります(時間が速ければ遠い:時間が遅ければ近い)。
時間 距離
だ び だ び
20:30(2:3)→逆比→1/2:1/3=3:2
だろうとびばりの時間の比が2:3なので、距離の比は(逆比で)
3:2になります。
距離が500mで、距離の比がだろう「3」でびばり「2」ですので、
だろうが300mいくとびばりは200mですから、ピッタリですね。
答え)300m
反比例:積が同じでともに変わる2つの量は逆比になる
「反比例:積が同じでともに変わる2つの量は逆比になる」
なんか、国語の難しい評論文のようですが、長方形の面積の問題で考えてください。
積(面積)が同じなら、縦×横が同じという事ですよね?
例えば縦3×横4=12の長方形
縦の長さが3:4の比で増えたとしましょう。その時、横の比は逆比になります。
3:4→逆比→1/3:1/4:4:3
縦の長さが3:6の比で増えたら?横の比は?
3:6→逆比→1/3:1/6:2:1
縦3:4:6
横4:3:2
こういうのを反比例と言います。ポイントは、
●積が一定で片方が増えたら片方が減る(比率は逆比)●
です。分かりづらいですか?
典型的なパターンは、「長方形の面積」ですが、中学受験の問題としては
「歯車」系の問題があります。最初は分からなくてもよく考えることと、
「パターン」だと思うことで解けるようになるかと。
https://jugo-blog.com/math-guidance28
問題)鎌倉女子学院中学
歯数32の歯車Aと歯数□の歯車Bがかみあっています。歯車Aが
6分間で180回転するとき、歯車Bは8分間で320回転します。
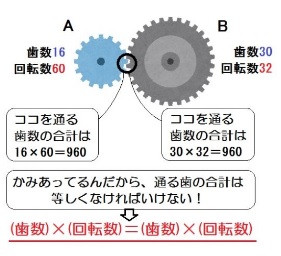
1分間でAは30回転、Bは40回転ですね?
(同じ時間の)「歯数×回転数」の積は一定になります。
という事は、
32×30=□×40
960=□×40 □=24
となります。また、この問題は「逆比」でも解けます。
積が一定なので、歯車の数と回転数は逆比になります。
回転数 歯車の数
30:40→逆比→4:3
4:3=32:24
答え)24
まとめ
若干小難しい所もありますが、逆比の基本を体で覚えて、
●面積、食塩水問題、速さと時間、仕事算etc
といった問題で、「逆比で解くと速い」という事を体験すると分かって
来る気がします。
逆比とは「逆数」の比の事です。
【逆数とは、その数にかけると1になる数】
です。2なら1/2、3なら1/3、15なら1/15ですね?

上の図でも分かるように、
2:5→逆比→5:2というのはあくまでも「結果」であって、
【2:5→逆比→1/2:1/5→1/2×(2×5):1/5×(2×5)→5:2】
というのが「分かっている」理解の仕方です。
逆比とは「逆数」(かけたら「1」になる数字)の比
の事です。
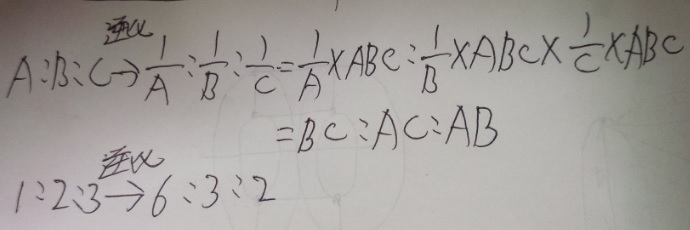

例えば、
「ある金額で、ジュースなら90本、サンドイッチなら36個、ケーキならば40個買える」
といった場合、それぞれ1個当たりの金額の比は個数の比の逆比になります。
簡単に考えると、1000円持っていて、ジュースなら10本(1本あたり100円)、サンドイッチ
なら5個(1個当たり200円)、ケーキなら2個(1個当たり500円)
買えるなら、それぞれ1個当たりの金額の比は個数の比の逆比になりますというのが分かりますよね?
個数 1個あたりの金額
10:5:2→逆比→1/10:1/5:1/2=1:2:5
慣れた場合(基本が完璧なら)2つの数字は、比率はひっくり返しても良いです。
(関連記事)
食塩水問題(濃度算)は2つ分かれば解ける!ビーカーの図・面積図を描け!