場合の数③順列の公式:A個からB個選んで並べる→Aから始め1つずつ数を減らしてB個掛け算
場合の数④組み合わせの公式:A個からB個選んで組み合わせる→①順列を計算②①をB個の並べ替え数で割る
(場合の数の)【組み合わせ】の考え方
●順列-ダブり部分●
(場合の数の)【組み合わせ】の公式
【A個からB個選んで組み合わせる→①順列を計算②①をB個の並べ替え数(順列)で割る
「順列」と「組み合わせ」の違い
場合の数の「組み合わせ」を理解するには、「順列」を分かっている必要があります。
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
シンプルに2人で考えて見ましょう。
だろう君とびばりさんがいます。
(1)二人の並べ方は何通り?(順列)
だろうーびばり、びばりーだろう 2通り
(2)二人の組み合わせは何通り(組み合わせ)
「だろう」と「びばり」だけですから、順番が逆になっても組み合わせは1つ。1通り。
(場合の数の)【組み合わせ】の考え方
●順列-ダブり部分●
(場合の数の)【組み合わせ】の公式
【A個からB個選んで組み合わせる→①順列を計算②①をB個の並べ替え数で割る
①順列:2通り ②2×1=2 2÷2=1
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
じゃあ、A、B、Cの「3人」
(1)3人の並べ方は何通り(順列)
A-B B-A C-A
-C -C -B
3×2=6 6通り。
【A個からB個選んで並べる→Aから始め1つずつ数を減らしてB個掛け算をする】
●A×(A-1)×(A-2)×・・・・(A-B+1)通り●
でしたね?
場合の数③順列の公式:A個からB個選んで並べる→Aから始め1つずつ数を減らしてB個掛け算
(2)3人の組み合わせは?
A/B/Cの1通りです。B/C/AもC・A・Bも「組み合わせ」は同じですよね?
【場合の数の「組み合わせ」の公式】
(場合の数の)【組み合わせ】の考え方
●順列-ダブり部分●
(場合の数の)【組み合わせ】の公式
【A個からB個選んで組み合わせる→①順列を計算②①をB個の並べ替え数(順列)で割る
A個からB個を選んで並べる順列
―――――――――――――――
選んだB個の並べ方
①6通り ②3個の並べ替え数は3×2×1=6 6÷6=1通り。
答え〕1通り
「順列」は「並べ方」の事で、
【A個からB個選んで並べる→Aから始め1つずつ数を減らしてB個掛け算をする】
でしたね?
場合の数③順列の公式:A個からB個選んで並べる→Aから始め1つずつ数を減らしてB個掛け算
「組み合わせ」は「並べ方」(順列)からダブった部分を引くというイメージです。
順列(並べ方)はすべてのパターン!【組み合わせ】はごちゃっとひとまとめに
して袋にほおりこむというイメージです。
問題)10人の生徒がいます。
(1)3人を選んだ場合の並べ方は何通り?
(2)3人の組み合わせは何通り
1、2、3、4、5、6、7、8、9、10
(1)3人を選んだ場合の並べ方→順列ですね?
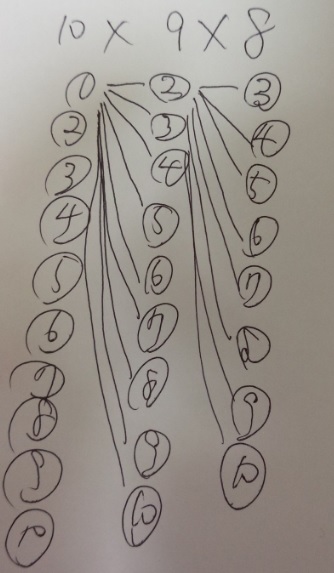
【A個からB個選んで並べる→Aから始め1つずつ数を減らしてB個掛け算をする】
10×9×8=720
1列目10通り、2列目9通り、3列目8通り、【3人】を選ぶのでここまでを掛け算する
答え)720通り
(2)3人の組み合わせは何通り
文字通り【組み合わせ】です。

1-2-3で考えてみましょう。
1)組み合わせは1通りです
2)並べ方(順列)は3×2×1=6通りです
1-2-3、1-3-2
2-1-3、2-3-1
3-1-2、3-2-1
6÷6=1ですね?
(場合の数の)【組み合わせ】の考え方
●順列-ダブり部分●
(場合の数の)【組み合わせ】の公式
【A個からB個選んで組み合わせる→①順列を計算②①をB個の並べ替え数(順列)で割る
A個からB個を選んで並べる順列
―――――――――――――――
選んだB個の並べ方
①720通り ②720÷(3×2×1)=120
答え)120通り
式で表すと、
10×9×8
―――― =120
3×2×1
になります。
【場合の数+組み合わせ】の場合、この形の式が基本となる
ので覚えましょう。
難しい言葉を使うと
A個からB個を選んで並べる順列
―――――――――――――――
選んだB個の並べ方
となります。
答え)(1)720通り(2)120通り
問題)A、B、C、D、Eの5人の中から2人の書記を選ぶとき、選び方は全部で何通りありますか。
「組み合わせ」ですね?「AとB」も「BとA」も同じというパターンです。
①順列を計算:5×4=20通り(2人なので1列目と2列目のみ)
②【2人】の並び替え数(順列)で割る:20÷2=10
答え)10通り
慣れるまでは樹形図を書きましょう。
場合の数の「組み合わせ」のテクニック!【少ない方を考える】
文字通り「少ない方を考える」というテクニックです。
問題)コーラ、ファンタ、カルピス、マンゴージュースがあります。
3つ選んで飲めます。何通りの組み合わせがありますか?
面倒なので数字にしましょう。
【少ない方】は飲まない1つですね?
1 2 3 4
1 2 3 4
1 2 3 4
1 2 3 4
答え)4通り
もちろん「組み合わせ」の公式を使っても計算できます。
①順列を出す:4×3×2×1=24
②選ぶ数(3)の並び替え数(6)で割る:24÷6=4
場合の数:組み合わせの公式の中学入試問題等
問題)立教池袋中学
お父さんとお母さんと4人の子供が遊園地に行き、3人乗りのコーヒーカップに
3人だけで乗ることにしました。次の問いに答えなさい。
(1)1台のコーヒーカップに子供だけで乗る乗り方は何通りありますか?
(2)1台のコーヒーカップにお父さんかお母さんのどちらかと子供が
いっしょに乗る乗り方は何通りありますか?
(1)について。
1)子供の数は4人
2)乗るのは3人
3)名前等は関係なし→組み合わせ(順列ではない)
4)解き方は2つ、「組み合わせ」「(組み合わせの)少ない方を考える」
「(組み合わせの)少ない方を考える」の解法
・4人の子供だけで3人乗りに乗る=乗らない子供は一人
1 2 3 4
1 2 3 4
1 2 3 4
1 2 3 4
「234」「134」「124」「123」の4通り。
「組み合わせ」の解法
【A個からB個選んで組み合わせる→①順列を計算②①をB個の並べ替え数(順列)で割る
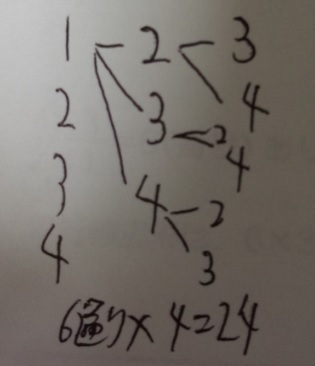
①順列を計算:4×3×2×1=24
②3個(人)の並べ替え数:3×2×1=6、24÷6=4
答え)4通り
(2)1台のコーヒーカップにお父さんかお母さんのどちらかと子供が
いっしょに乗る乗り方は何通りありますか?
1)4人の子供のうち2人が必ず乗っているので、
4人から2人を選ぶ組み合わせは、4×3=12(順列)を2人の並び替え数(2)
で割るので、12÷2=6通り。
1 2 3 4
1 2 3 4
1 2 3 4
1 2 3 4
1 2 3 4
1 2 3 4
2)この6通りに、父か母のどちらかが乗っている組み合わせは、
「それぞれ+父」「それぞれ+母」なので6×2=12
1 2+父、+母
1 3+父、+母
1 4+父、+母
2 3+父、+母
3 4+父、+母
2 4+父、+母
答え)12通り
答え)(1)4通り、(2)12通り
場合の数④組み合わせの公式―まとめ
(場合の数の)【組み合わせ】の考え方
●順列-ダブり部分●
(場合の数の)【組み合わせ】の公式
【A個からB個選んで組み合わせる→①順列を計算②①をB個の並べ替え数(順列)で割る
A個からB個を選んで並べる順列
―――――――――――――――
選んだB個の並べ方
場合の数③順列の公式:A個からB個選んで並べる→Aから始め1つずつ数を減らしてB個掛け算
場合の数④組み合わせの公式:A個からB個選んで組み合わせる→①順列を計算②①をB個の並べ替え数で割る