場合の数③順列の公式:A個からB個選んで並べる→Aから始め1つずつ数を減らしてB個掛け算
場合の数④組み合わせの公式:A個からB個選んで組み合わせる→①順列を計算②①をB個の並べ替え数で割る
「場合の数」の意味は「起こり方が何通りあるか」を求める事です。
●場合の数の解き方の方法●
1)樹形図を書く
2)表を書く
3)計算をする(順列)
●場合の数の解き方のポイント●
・「書き出し」は正確に丁寧に
・「書き出し」に慣れる
この記事では、「場合の数」の問題で「表を書く」パターンを
確認していきます。
「場合の数」の問題で「表を書く」パターン
●「2人の~」「2つの~」といった表現の問題の時●
→「表」の書き方に慣れましょう!!!
(関連記事)場合の数①樹形図を使うパターン
場合の数で表を使うパターン
「場合の数」の問題で「表を書く」パターン
●「2人の~」「2つの~」といった表現の問題の時●
→「表」の書き方に慣れましょう!!!
問題)2つのサイコロを同時に投げる時、出る目の数の和が3の
倍数になるのは全部で何通りありますか?
●「2人の~」「2つの~」といった表現の問題の時●
なので「表」を使ってみます。

答え)12通り
問題)大小2つのサイコロを同時に投げます。
(1)目の数の和が7になる
(2)目の数の積が3の倍数になる
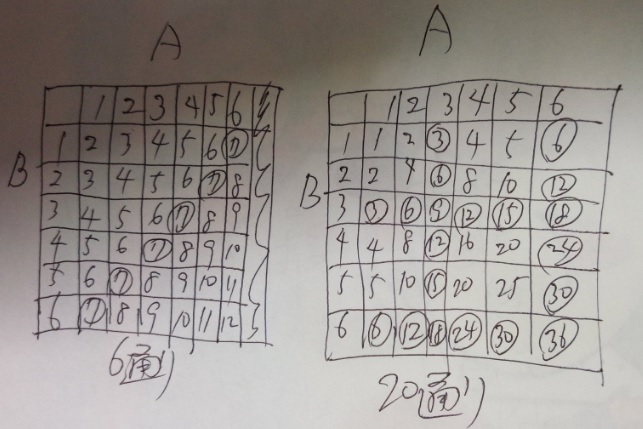
答え)(1)6通り (2)20通り
問題)だろう君は1、2、3、4、5、6の数字が書かれた6枚の
カードを持っています。びばりさんは1、3、5、7、9の数字が
書かれた5枚のカードを持っています。2人が1枚ずつカードを出し
あったとき、2人のカードの数の積が10以下となるのは全部で
何通りですか?
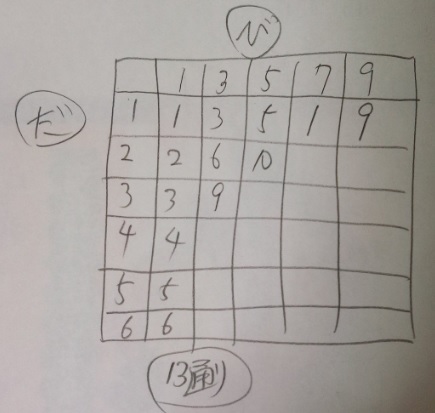
答え〕13通り
シンプルな掛け算なので、11以上になるところはわざわざ計算しなくてもいいでしょう。
問題)A、B、C、Dの4つのチームで、サッカーの総当たり戦をします。
試合の組み合わせは何通りになりますか?
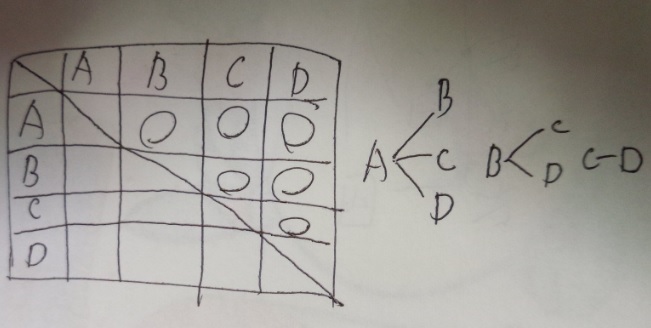
答え)6通り
「総当たり」の試合数=(チーム数-1)×チーム数÷2
「トーナメント」の試合数=「参加数-1」
上記は「総当たり」ですが、甲子園の高校野球のように
「トーナメント戦」(下図)の場合、全試合数は「参加数-1」
になります。考え方は、
【「1チーム(ないしは一人)が負けるのに1試合」
なので、優勝チームが決まる=優勝チーム以外がすべて負ける】
という事になります。
場合の数で表を使うパターンの中学入試問題等
問題)城北中学
A~Fの6つのサッカーチームが、総当たりの試合を行った。引き分けの試合は
なく、勝ち数で順位をつけたところ次の4つの事が分かった。
ア:BとEが同じ勝ち数で1位であった イ:Fは単独で3位であった
ウ:CはEに勝った エ:CはAに負けて単独4位であった
(1)A~Fの6チームでの試合数は全部で何試合ですか?
(2)①C対D ②A対Dの2つの対戦で勝ったのはどっちのチームですか?
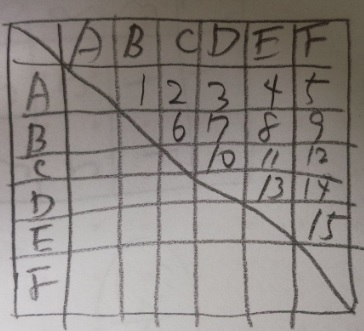
(1)15試合
表を書いても良いですし、以下の考え方を覚えても良いです。
6チームの総当たりなので、各チーム5試合します。
A対BとB対Aは同じ試合なので、5×6÷2=15
(2)①C ②D
順位を確認します。
1位(2チーム) BとEで同じ勝ち数
3位 F
4位 C
5位、6位 AとD
★ウ:CはEに勝った→BとEは5勝はしない(4勝以下)
同時に、BとEが3勝だと、残りの勝ち数は15-6=9となり、
F2勝、C1勝、A,D0勝では計算が合わない。
よって、B,Eは4勝1敗と分かる。
また、引き分けは存在しないので、AとDも0勝ではない。
となると、15-8=7勝が残り、
FとCとAとDが3勝、2勝、1勝、1勝と分かる。
整理すると
B,Eは4勝1敗
F 3勝2敗
C 2勝3敗
AとD 1勝4敗
これを表に書き込む。

(2)①C対D ②A対Dの2つの対戦で勝ったのはどっちのチームですか?
①C ②D
答え)(1)15試合 (2)①C ②D
まとめ
●場合の数の解き方の方法●
1)樹形図を書く
2)表を書く
3)計算をする(順列)
●場合の数の解き方のポイント●
・「書き出し」は正確に丁寧に
・「書き出し」に慣れる
「場合の数」の問題で「表を書く」パターン
●「2人の~」「2つの~」といった表現の問題の時●
→「表」の書き方に慣れましょう!!!
「総当たり」の試合数=(チーム数-1)×チーム数÷2
「トーナメント」の試合数=「参加数-1」
場合の数③順列の公式:A個からB個選んで並べる→Aから始め1つずつ数を減らしてB個掛け算
場合の数④組み合わせの公式:A個からB個選んで組み合わせる→①順列を計算②①をB個の並べ替え数で割る