場合の数③順列の公式:A個からB個選んで並べる→Aから始め1つずつ数を減らしてB個掛け算
場合の数④組み合わせの公式:A個からB個選んで組み合わせる→①順列を計算②①をB個の並べ替え数で割る
「場合の数」???意味が分からん。読み方も分からん。
読み方は「ばあいのかず」が基本のようですが、人によっては
「ばあいのすう」と言っていますね…。共用(どちらでもいい)なの
かな?英語で言う”Either will do”ってやつですかね。
はい、「場合の数」の意味は「起こり方が何通りあるか」を求める事です。
●場合の数の解き方●
1)樹形図を書く
2)表を書く
3)計算をする(順列)
●場合の数の解き方のポイント●
・「書き出し」は正確に丁寧に
・「書き出し」に慣れる
・「金額」系の場合、大きい金額のものから書きだしていく
この記事では「樹形図」を使う方法を覚えましょう。
場合の数の基本
「場合の数」の意味は「起こり方が何通りあるか」を求める事です。
●場合の数の解き方の方法●
1)樹形図を書く
2)表を書く
3)計算をする(順列)
●場合の数の解き方のポイント●
・「書き出し」は正確に丁寧に
・「書き出し」に慣れる
・「金額」系の場合、大きい金額のものから書きだしていく
問題)1,2,3の数字が書かれた紙がそれぞれ1枚ある場合、
2枚を選んで2桁の数字を作ると何通りの数字を作れますか?
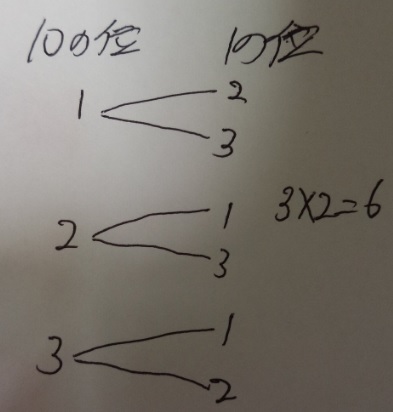
答え)6通り
問題)サイコロ2つを転がした時に2つの目の積が6になるのは何通り?
サイコロA サイコロB
1 → 6
2 → 3
3 → 2
4 → ×
5 → ×
6 → 1
答え)4通り
問題)だろう君とびばりさんとごんた君がじゃんけんをします。
だろう君だけが勝つのは何通りありますか?
だろう びばり ごんた
グー → ち ち
チョキ→ ぱ ぱ
パー → ぐ ぐ
答え)3通り
問題)だろう君とびばりさんとごんた君がじゃん
けんをします。だろう君が勝つのは何通りありますか?
「だろう君が勝つ」です。「だろう君だけが勝つ」ではありません。
でも「だろう君だけが勝つ」の3通りを使えそうです。
だろう びばり ごんた
グー → ち ち 1
ぐ 2
ぐ ち 3
チョキ→ ぱ ぱ 4
ち 5
ち ぱ 6
パー → ぐ ぐ 7
ぱ 8
ぱ ぐ 9
いきなり「だろう君が勝つ場合」といわれたら、まさに「場合」を
きちんと樹形図に書きましょう。「だろうが勝つ」場合は、
「だろうだけ」「だとうとびばりが勝つ」「だろうとごんたが勝つ」の3通りだけです。
1)だろう君だけが勝つ
だろう びばり ごんた
グー → ち ち
チョキ→ ぱ ぱ
パー → ぐ ぐ
2)だろう君とびばりが勝ち、ごんたが負ける
だろう びばり ごんた
ぐ ぐ ち
ち ち ぱ
ぱ ぱ ぐ
3)だろうとごんたが勝ち、びばりが負ける
だろう びばり ごんた
ぐ ち ぐ
ち ぱ ち
ぱ ぐ ぱ
答え)9通り
問題)0、1、2、3、4の5枚のカードがあります。このカードを
使って3桁の整数を作る場合、何通りありますか?
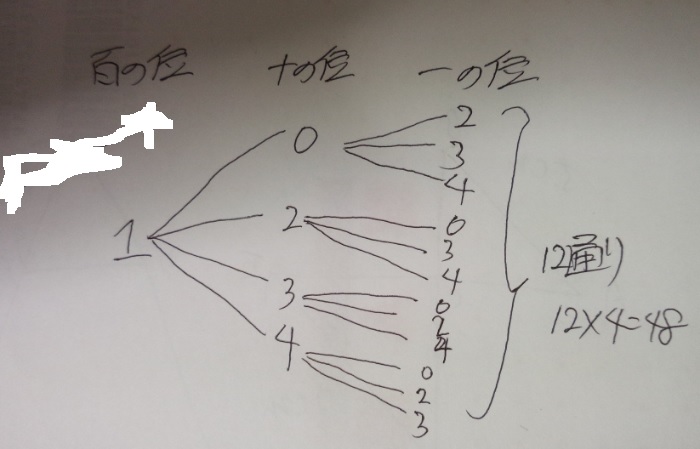
答え〕48通り
*樹形図は繰り返しの要素があれば、それをかけ算によって処理することができます。
(場合の数③順列で使う公式はまさにそれです)
問題)10円玉6枚、50円玉4枚、100円玉5枚があります。
それを使って560円にする方法は何通りありますか?
(使わない硬貨があっても構いません)
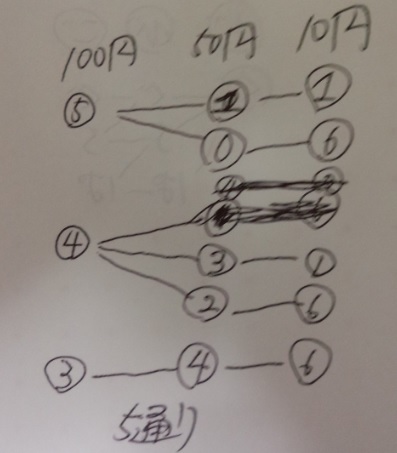
・「金額」系の場合、大きい金額のものから書きだしていく
計算がしやすいからです。
答え)5通り
場合の数①樹形図を使うパターンの中学受験問題等
問題)明治学院中学
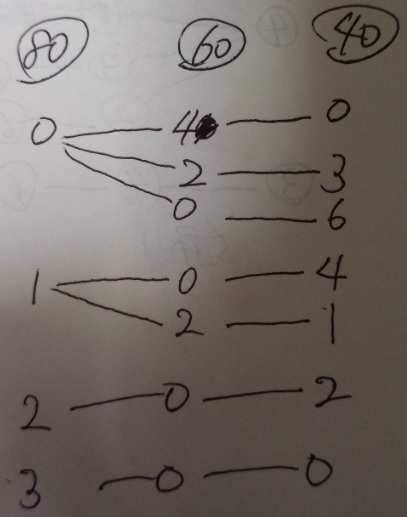
40円、60円、80円切手を使って、送料240円の荷物を送ります。切手を
ちょうど240円分使う時、次の問いに答えなさい。
(1)40円切手を必ず使う事にすると、切手の使い方は何通りありますか?
(2)どの切手を使っても良いことにすると、切手の使い方は何通りありますか?
問題)早稲田実業中等部
みかんが3個、りんごが3個、メロンが1個、柿が2個あります。この中から
同時に3個取り出すとき、取り出し方は何通りありますか。ただし、同じ
種類のくだものを取ってもよいこととします。
このパターンは樹形図がピッタリです。3個取り出すので、みかんとりんごが
全てのパターンがありますね?そういった前提を立てて書いていく事も
大事です。
考えてみましょう。
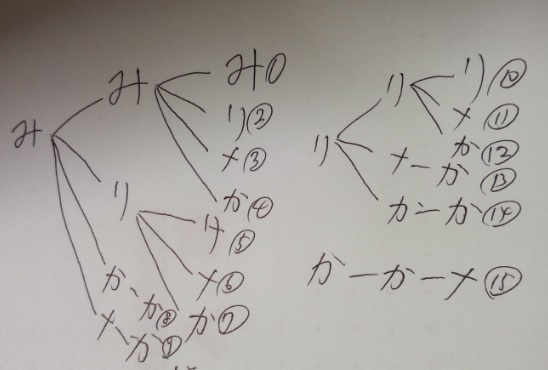
答え〕15通り
・「書き出し」は正確に丁寧に
・「書き出し」に慣れる
まとめ
●場合の数の解き方●
1)樹形図を書く
2)表を書く
3)計算をする(順列)
●場合の数の解き方のポイント●
・「書き出し」は正確に丁寧に
・「書き出し」に慣れる
・「金額」系の場合、大きい金額のものから書きだしていく
「場合の数」に限った話ではありませんが、
問題のパターンに慣れて、解き方に慣れる
これが受験勉強の王道です。
どれくらい慣れれば良いのかって?
飽きるほどですかね。
樹形図は繰り返しの要素があれば、それをかけ算によって処理することができます。
(場合の数③順列で使う公式はまさにそれです)
場合の数③順列の公式:A個からB個選んで並べる→Aから始め1つずつ数を減らしてB個掛け算
場合の数④組み合わせの公式:A個からB個選んで組み合わせる→①順列を計算②①をB個の並べ替え数で割る