場合の数③順列の公式:A個からB個選んで並べる→Aから始め1つずつ数を減らしてB個掛け算
場合の数④組み合わせの公式:A個からB個選んで組み合わせる→①順列を計算②①をB個の並べ替え数で割る
この記事は「場合の数+整数の数字作り」のパターンについてまとめます。
基本的には「順列」の一種となります(先に「順列」の記事を読んでください)。
★「場合の数+整数の数字作り」のパターン★
1)順列の問題として解く(「0」を含まない問題)
2)(「0」を含む問題は)一番上の位は「0」にならない事に注意!
3)「「3」の倍数」系の問題:各位の数の和が「3」又は「9」の倍数になるようにする
4)「偶数・奇数」「5or10の倍数」系の問題:1の位をまず決める
「場合の数+整数の数字作り」のパターン1:「0」を含まない
問題)1,2,3,4の4枚のカードから3枚を取り出して3桁
の整数を作ると何通りの整数ができますか?
典型的な「場合の数+整数の数字作り」の問題です。「順列」を使います。
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
A個の異なるものから、異なるB個を選んで並べる順列の公式
●A×(A-1)×(A-2)×・・・・(A-B+1)通り●
(難しいので…以下でもOK)
【A個からB個選んで並べる→Aから始め1つずつ数を減らしてB個掛け算をする】
場合の数③順列の公式:A個からB個選んで並べる→Aから始め1つずつ数を減らしてB個掛け算
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
でしたね?
4×3×2=24 24通り。慣れたら樹形図なしでも良いですが、最初は書きましょう。
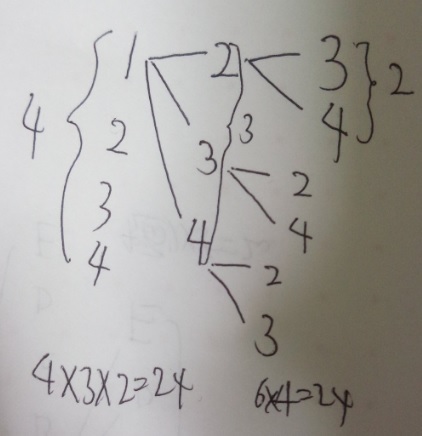
答え)24通り
★「場合の数+整数の数字作り」のパターン★
1)順列の問題として解く(「0」を含まない問題)
2)(「0」を含む問題は)一番上の位は「0」にならない事に注意!
3)「「3」の倍数」系の問題:各位の数の和が「3」又は「9」の倍数になるようにする
4)「偶数・奇数」「5or10の倍数」系の問題:1の位をまず決める
「場合の数+整数の数字作り」のパターン2:(「0」を含む問題は)一番上の位は「0」にならない事に注意!
問題)0,1,2,3,4の5枚のカードから3枚を取り出して
3桁の数字を作る場合、何通りの方法がありますか?
「パターン1」と違うのは「0」が入っている事です。
「3桁の数字」なので、「0」が100の位(一番上の位)には来ません。
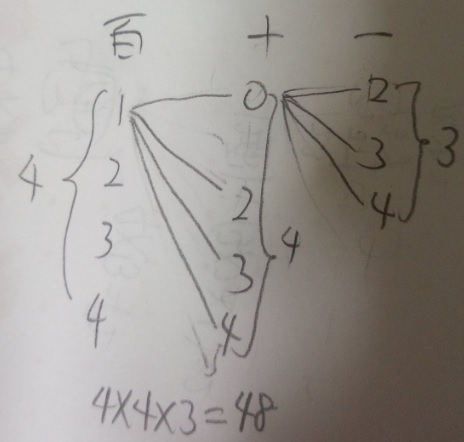
樹形図を良く見てください。
1)100の位:「0」が使えませんので、1,2,3,4の4通り
仮に100の位を「1」とします。
2)10の位:「0」使えます。0,2,3,4の4通り
仮に10の位を「0」とします。
3)1の位:(1と0を既に使っているので)2,3,4の3通り
よって、4×4×3=48
答え)48通り
「0」が絡む「数字作り系の問題」は「一番上の位に「0」が来ない」のが
ポイントです。その上で樹形図を作ればそれほど難しくないのでは?
「式」としては、A×A×(A-1) 的なものになります。順列の基本は
A×(A-1)×(A-2)でしたよね?
★「場合の数+整数の数字作り」のパターン★
1)順列の問題として解く(「0」を含まない問題)
2)(「0」を含む問題は)一番上の位は「0」にならない事に注意!
3)「「3」の倍数」系の問題:各位の数の和が「3」又は「9」の倍数になるようにする
4)「偶数・奇数」「5or10の倍数」系の問題:1の位をまず決める
「「3」の倍数」系の問題:各位の数の和が「3」又は「9」の倍数になるようにする
「「3」の倍数」系の問題:各位の数の和が「3」又は「9」の倍数になるようにする
【「3」の倍数】は大丈夫ですよね?(まだの人は下記記事をどうぞ)
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
倍数判定法(2,3,4,5,6,8,9,10,11,12)/算数・youtube音声動画付き
「3」の倍数はそれぞれの位の数字を全部足した数が「3」の倍数になる数字です。
12→1+2=3
15→1+5=6
27→2+7=9
123→1+2+3=6
1008→1+0+0+8=9
2481→2+4+8+1=15
4584→4+5+8+4=21
123456789→1+2+3+4+5+6+7+8+9=45
(「1+9」+「2+8」+「3+7」+「4+6」+「5」)
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
「「3」の倍数」系の問題:各位の数の和が「3」又は「9」の倍数になるようにする
問題)1,2,3,4、5の5枚のカードから3枚を取り出して3桁
の整数を作る時、3の倍数は何通りできますか?
「3」の倍数ですから、「百の位+十の位+一の位=3の倍数」です。
最も小さい数字は「123」です。あ、「6」なので3の倍数ですね?
最も大きい数字は「543」です。あ、「12」なので3の倍数ですね?
という事は、3つの数字の合計が「6」「9」「12」になるパターンです。
「6」:「123」の並べ替えなので、3×2×1=6通り(123、132、213、231、312、321)
「9」:「135」の並び替えなので3×2×1=6通り
:「234」も【9】になる。3×2×1=6通り
「12」:「345」の並び替えなので3×2×1=6通り
6×4=24 答え)24通り
「「3」の倍数」系の問題:各位の数の和が「3」又は「9」の倍数になるようにする
★「場合の数+整数の数字作り」のパターン★
1)順列の問題として解く(「0」を含まない問題)
2)(「0」を含む問題は)一番上の位は「0」にならない事に注意!
3)「「3」の倍数」系の問題:各位の数の和が「3」又は「9」の倍数になるようにする
4)「偶数・奇数」「5or10の倍数」系の問題:1の位をまず決める
「偶数・奇数」「5or10の倍数」系の問題:1の位をまず決める
「偶数・奇数」「5or10の倍数」系の問題:1の位をまず決める
問題)昭和学院秀英中学
0,1,2,3,4の5枚のカードから3枚を取り出して3桁
の整数を作る時、
(1)全部で何通り作れますか?
(2)偶数は何通りできますか?
(1)について、「0」が入ってますので、
4×4×3=48
答え)48通り

(2)偶数は何個ですか?
「偶数・奇数」「5or10の倍数」系の問題:1の位をまず決める
【偶数】という事は「一の位が偶数」という事です。
0か2か4ですね?
樹形図に一の位から決めるのが基本です。
ただし、この問題では「0」がありますので、百の位には「0」が
使えない事を見落としてはいけませんよ。
ですので、この問題は、
●「1の位が0の時」と「1の位が2と4の時」の場合に分けましょう●
「1の位が0の時」は12通り
百 十 一
0
百 十 一
1~4 0
百 十 一
0と十の位以外の3つ 1~4 0
「3」 「4」 「1」
3×4×1=12 12通り
「1の位が2と4の時」は9通り×2=18通り
(一の位を2でやります)
百 十 一
2
百 十 一
1,3,4 2
百 十 一
1,3,4 2と百の位以外の3つ 2
3×3×1=9
先に100の位を出してしまった方が楽です。もちろん、
樹形図に丁寧に書いた方が安心かもしれません。

答え)30通り
答え)(1)48通り(2)30通り
場合の数⑤整数の数字作りのパターンの中学受験問題等
問題)洛南中学
1,2,3,4の4枚のカードのうち、3枚のカードを並べて3桁の数字を作ります。
作る事のできる数のうち6の倍数になるのは全部で□個あります。
1)「6」の倍数なので、「2の倍数かつ3の倍数」ですね?
2の倍数は偶数なので1の位で分かります。3の倍数かどうかは3つの位を全部足します。
倍数判定法(2,3,4,5,6,8,9,10,11,12)/算数・youtube音声動画付き
2)2の倍数で小さいものは、124、132辺りです。132が6の倍数ですね
6の倍数になる一番小さい数字が132です。3つの数字を足すと「6」
3)偶数で一番大きいのは、432です。3つの数字を足すと「9」なので、6の倍数ですね。
という事は、3つの数字を足して「6」「9」になる+偶数が条件に合致します。
132の並び替えは「123、132、213、231、312、321」の6通り。偶数は2通り。
432の並び替えは「432、423、324、342、234、243」の6通り。偶数は4通り。
足すと6通り
答え)6
「2の倍数」はすぐに分かるので、「3の倍数になる偶数末尾の組み合わせ」を
先に考えて(132、432)その並び替えに何個偶数があるかを考えると速く解ける
かもしれません。
まとめ
★「場合の数+整数の数字作り」のパターン★
1)順列の問題として解く(「0」を含まない問題)
2)(「0」を含む問題は)一番上の位は「0」にならない事に注意!
3)「「3」の倍数」系の問題:各位の数の和が「3」又は「9」の倍数になるようにする
4)「偶数・奇数」「5or10の倍数」系の問題:1の位をまず決める
場合の数③順列の公式:A個からB個選んで並べる→Aから始め1つずつ数を減らしてB個掛け算
場合の数④組み合わせの公式:A個からB個選んで組み合わせる→①順列を計算②①をB個の並べ替え数で割る